Lecture
1. Linear programming tasks.
The task of the diet (the task of the hostess, the task of the soldier's canteen).
There are four types of food: P 1 , P 2 , P 3 , P 4 . The known unit cost of each product: С 1 , С 2 , С 3 , С 4 . From these products it is necessary to make a diet, which should contain:
- proteins of at least b 1 units,
- carbohydrates of at least b 2 units,  (*)
(*)
- fat not less than b 3 units.
A unit of product P 1 contains a 11 , units of proteins, a 12 units of carbohydrates, a 13 units of fat, etc.
It is required to make a food ration so as to provide a condition (*) at the minimum cost of products. We construct the model of the IO problem. Denote x 1 , x 2 , x 3 , x 4 the number of products included in the diet. The total cost will be:
L = c 1 x 1 + c 2 x 2 + c 3 x 3 + c 4 x 4 or
L = 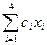 .
.
We write the conditions for proteins, fats and carbohydrates
a 11 x 1 + a 21 x 2 + a 31 x 3 + a 41 x 4 b 1 ;
a 12 x 1 + a 22 x 2 + a 32 x 3 + a 42 x 4 b 2 ; 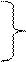
a 13 x 1 + a 23 x 2 + a 33 x 3 + a 43 x 4 b 3 .
These conditions are constraints imposed on the solution.
Thus, the following IO problem arises: choose non-negative values of variables x 1 , x 2 , x 3 , x 4 (vectors (x 1 , x 2 , x 3 , x 4 )) satisfying the system of linear inequalities (**), with which linear function of these variables
L = c 1 x 1 + c 2 x 2 + c 3 x 3 + c 4 x 4
would appeal to the minimum.
With some modifications, this task is called the soldering problem. Usually, restrictions are added to it:
- the weight of the soldering should not exceed a given value of p,
- the ration should be the minimum volume.
Sometimes (for soldering) the target function and limitation are interchanged:
- the cost of rations should not exceed C monetary units;
- the ration should have a maximum caloric content.
It is assumed that for the unit of each product Pk, the volume vk, the weight pk and the caloric value qk are known.
The problem of resource allocation.
There are some resources (raw materials, labor, equipment, information):
R 1 , R 2 , ..., R m in appropriate quantities: b 1 , b 2 , ..., b m units.
With the help of these resources, final products (goods) can be produced:
T 1 , T 2 , ..., T n .
For the production of one commodity unit T j, it is necessary a ij resource units R i (i = 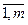 j =
j = 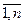 ). Each unit of resource R i costs d i hryvnia (i =
). Each unit of resource R i costs d i hryvnia (i = 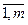 ). Each item can be sold at a price c j (j =
). Each item can be sold at a price c j (j = 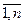 ).
).
For each type of product, the number of units produced is limited by demand: the market cannot absorb more than k j units of goods T j (j = 1, 2, ..., n).
How many units of a product need to be produced in order to get the maximum profit?
Denote by x 1 , x 2 , ..., x n the number of goods T 1 , T 2 , ..., T n planned for production. The conditions of demand impose the following restrictions:
x 1 k 1 ; x 2 k 2 ; ...; x n k n .
There should be enough resources, hence the limitations:
a n1 x 1 + a 12 x 2 +… + a 1n x n b 1 ;
a 21 x 1 + a 22 x 2 +… + a 2n x n b 2 ; 
. . . . . . . . . .
a m 1 x 1 + a m 2 x 2 +… + a mn x n b m .
Or in a shorter form:
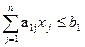 ;
;
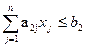 ;
; 
. . . . . .
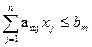
Find the expression for profit: the unit cost of goods T j is equal to:
S j = a 1j d 1 + a 2j d 2 +… + a mj d m ,
or
S j = 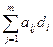 (j =
(j =  ).
).
Calculate the cost of goods of each type: S 1 , S 2 , ..., S n .
The net profit q j for a product T j is equal to the difference between the sale price C j and the cost price S i :
q j = C j - S j , (j = 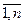 ).
).
Net profits: q 1 , q 2 , ..., q n .
Total profit (objective function):
L = q 1 x 1 + q 2 x 2 +… + q n x n ,
or shorter:
L = 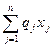 .
.
Choose such non-negative values of the variables x 1 , x 2 , ..., x n that satisfy linear inequalities and maximize the linear function L.
2. Problems of discrete programming.
A special class of problems consists of discrete programming problems, in which the set of solutions is discrete or in particular integer.
Old Russian task.
How much should Grandma take to the market to sell live geese, ducks and chickens in order to gain as much money as possible if she can take goods weighing no more than P kg. It is known that a 1 is the mass of one chicken, a 2 is the mass of one duck, a 3 is the mass of one goose, c 1 , c 2 and c 3 are their corresponding values.
Let x 1 , x 2 , x 3 be the number of hens, ducks and geese, respectively, taken for sale. Target function:
c 1 x 1 + c 2 x 2 + c 3 x 3 = 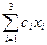
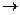 max.
max.
The limitation condition is the mass of goods that a grandmother can take:
a 1 x 1 + a 2 x 2 + a 3 x 3 P,
x 1 x 2 x 3 Z.
If desired, you can take into account market conditions.
The task of the backpack.
This is one of the most popular tasks of integer programming.
Tourist preparing for a long transition. In a backpack, he can carry a weight of not more than W kg. This load may include n kinds of objects, each item of type j, mass w j kg, j =. For each type of item, the tourist determines his value E j during the trip. How many items of each type should he put in his backpack so that the total value of the equipment is maximum?
Denote by x j - the number of items of the j - th type in the backpack. Then the mathematical model of the problem is as follows:
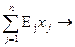 max
max
under restrictions:
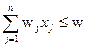 x j
x j 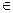 Z (integers).
Z (integers).
x j 0, j = 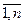 .
.
These are the so-called indivisibility problems (loading vehicles, fire evacuation plan).
3. Tasks of dynamic programming.
Task.
The owner of the car has operated it for m years. At the beginning of each year, he can take one of three decisions:
1) sell the car and replace it with a new one;
2) repair and continue operation;
3) continue operation without repair.
The choice of each of the three solutions - there is a step-by-step operation management (one step - once a year). The choice of each of the three solutions is not expressed numerically, but the first solution can be assigned the number 1, the second - 2, and the third - 3. How can we alternate the decisions by year, so that the total costs are minimal?
Additivity index:
W = 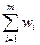 ,
,
where w i - expenses in the i-th year. W should be turned to a minimum. Management may be as follows:
x = (3, 3, 2, 2, 2, 1, 3, ...).
But in general this is a vector:
x = (j 1 , j 2 , ..., j m ),
where j 1 , j 2 , ..., j m can take the values 1, 2 or 3.
This is a special problem that belongs to the class of dynamic programming problems, which are solved step by step, and the criterion (or gain) is made up of the gains on individual steps:
W = 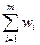
(additive criterion).
Half in lukewarm is half serious LN Tolstoy proposed a criterion for assessing the quality of a person. He had the appearance of a fraction, in the numerator of which are the dignity of a person, and in the denominator - his opinion of himself. This criterion is logical only at a glance.
( 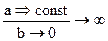 ).
).
4. Tasks on networks.
A special class of Io tasks are tasks on networks.
The transport problem solved in 1948 is considered as an example of a network or streaming problem. F.L. Hitchcock.
Transport task.
Suppose there are two factories and three warehouses. Plants produce, respectively, S 1 and S 2 units of production, the possibilities of warehouses - d 1 , d 2 , d 3 units
S 1 + S 2 = d 1 + d 2 + d 3
The task is to minimize the cost of transporting products from factories to warehouses. Let x ij be the volume of production that needs to be transported from the i-th plant to the j-th warehouse and c ij - the cost of transporting a unit of production from the i-th plant to the j-th warehouse.
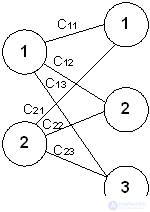
Then the objective function - the cost of transportation - has the form:
c 11 x 11 + c 12 x 12 + c 13 x 13 + c 21 x 21 + c 22 x 22 + c 23 x 23 = 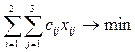
The condition that all products will be taken from each plant:
x 11 + x 12 + x 13 = 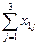 = S 1
= S 1
x 21 + x 22 + x 23 = 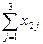 = S 2
= S 2
Or briefly: 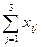 = S i ; i = 1,2.
= S i ; i = 1,2.
The condition for filling warehouses is:
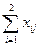 = d j ;
= d j ; 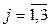
Basics of linear programming.
Formulation of a general linear programming (LP) problem and its analysis.
If the set of feasible solutions 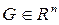 is a convex polyhedron, and the optimality criterion is a scalar linear objective function, then the problem is called the LP problem. Speaking about the LP problems, we actually mean not the IO problem itself, but its mathematical model with certain properties.
is a convex polyhedron, and the optimality criterion is a scalar linear objective function, then the problem is called the LP problem. Speaking about the LP problems, we actually mean not the IO problem itself, but its mathematical model with certain properties.
The task of the LP is as follows:
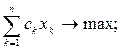
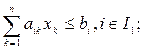
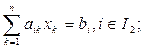
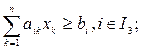
(2.1)
Where a ik , c k , b i are known numerical parameters, and the sets I 1 , I 2 , I 3 do not overlap in pairs and 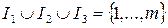 . Unknown x k ,
. Unknown x k , 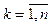 , representing the coordinates of the vector X (x 1 , x 2 , ..., x n ) T are called controlled variables or model variables.
, representing the coordinates of the vector X (x 1 , x 2 , ..., x n ) T are called controlled variables or model variables.
Consider an example.
The company produces two types of varnish for interior and exterior use. For the production of varnishes, two initial products are used - A and B. The maximum possible daily costs of these products are determined by the capacities that are available and are 6 and 8 tons, respectively. The production of 1 ton of lacquer for interior works consumes 1 ton of product A and 2 tons of product B, while the production of 1 ton of lacquer consumes external works 2 tons of product A and 1 ton of product B.
Market research has shown that the daily demand for outdoor varnish does not exceed 2 tons. Revenue from sales (in thousands of cu) of 1 ton of lacquer for interior work is 3, and revenue from the sale of 1t of varnish for exterior work is 2.
Determine how much varnish of each type the company should produce in order to maximize its sales.
The essence of this task IO can be defined as follows. It is necessary to determine the production volumes of each type of product taking into account restrictions on demand and taking into account the consumption of initial products A and B.
The controlled variables are x 1 - the daily volume of production of varnish for interior work, x 2 is the daily volume of production of varnish for outdoor work. Thus, n = 2.
The daily consumption of the initial products A and B cannot exceed the maximum daily supply, i.e. 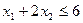 and
and 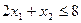 .
.
The limitation on the value of daily demand for outdoor varnish has the form. Since the volumes can not be negative, then. Thus, in problem (2.1), m = 3, I 1 = {1,2,3}, I 2 = I 3 = 0.
Total revenue f (x 1 , x 2 ) = 3x 1 + 2x 2 . The mathematical model of the considered IO problem can be represented as:
3x 1 + 2x 2 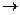 max
max
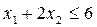 ,
,  ;
; 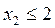 (2.2)
(2.2)
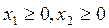
Comments
To leave a comment
Mathematical methods of research operations. The theory of games and schedules.
Terms: Mathematical methods of research operations. The theory of games and schedules.