Lecture
This section deals with games with two players, which will be referred to as MAX and MIN for reasons that will soon become apparent. The MAX player moves first, after which the players take turns in turns until the game ends. At the end of the game, the winning player is awarded points, and a penalty is imposed on the loser. A game can be formally defined as a sort of search task with the components described below.
The initial state and allowable moves of each side determine the game tree for this game. From the initial state, the MAX player has nine possible moves. The moves alternate in such a way that max puts X, a MIN mark O, until the leaf nodes corresponding to the terminal states are reached, such that one player leaves three of his badges in one row or all the cells are filled.
The number under each leaf node indicates the utility value of the corresponding terminal state from the player's point of view max; it is assumed that high values are favorable for the player MAX and unfavorable for the player MIN (which is why, in theory, these players are given such names). The MAX player’s task is to use a search tree (especially data on the usefulness of terminal states) to determine the best move.
Optimal strategists
When solving ordinary search problems, the optimal solution for the player MAX should be a sequence of moves leading to the goal - to the terminal state, which corresponds to the gain. On the other hand, the player MIN is also involved in the game, who has a different opinion on this. This means that the MAX player must find a reliable strategy to determine the MAH player’s move in the initial state, then the MAX player’s moves in the states resulting from any possible MIN player’s response, and then the MAX moves in the states that resulted from any possible MIN’s answer to moves, etc. Roughly speaking, the optimal strategy leads to a result that is at least as favorable as any other strategy, in those conditions when you have to play with an adversary who does not admit mistakes. First of all, let us consider how to find this optimal strategy, even though for MAX it will often be impossible to carry out its exhaustive computation in games that are more complicated than tic-tac-toe.
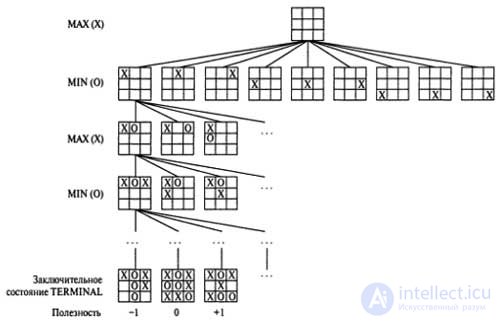 |
| (Partial) search tree for tic-tac-toe game. The top node represents the initial state, and the MAX player walks first, placing an X in an empty cell. This picture shows a part of the search tree in which alternating moves of players MIN (O icon) and MAX (X icon) are shown. The moves are performed until finally one of the terminal states is reached, which can be assigned utility data in accordance with the rules of the game. |
Even simple games such as tic-tac-toe are too complex to be able to bring the full game tree for them in this book, so let's move on to the description of the trivial game shown in the figure. Possible player codes MAX from the root node are labeled as ab2 and a3. Possible answers to ai for player MIN are b1, b2, b3, etc. This particular game ends after each player, MAX and MIN, makes one move each. (According to the terminology of game theory, this tree has a depth of one turn and consists of moves made by two participants, each of which is called a half-move.) The usefulness of the terminal states in this game ranges from 2 to 14.
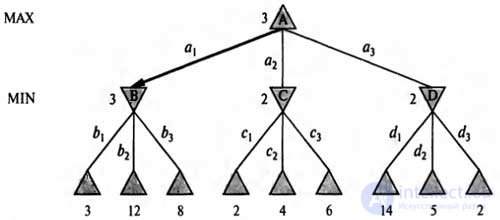 |
| Tree game with two semi-moves. Nodes A are "MAX nodes" in which the turn of turn belongs to the MAX player, and the nodes are considered as "MIN nodes". Terminal nodes show utility values for MAX; the remaining nodes are indicated by their minimax values. The best MAX player move from the root is a.1, because it leads to the successor with the highest minimax value, and the best answer MIN is hi, because it leads to the successor with the smallest minimax value |
If there is a game tree, the optimal strategy can be determined by examining the minimax value of each node, which can be written as Minimax-Value (n). The minimax value of a node is the utility (for MAX) of staying in the corresponding state, provided that both players make moves in an optimal way from this node to the node that marks the end of the game. Obviously, the minimax value of the terminal state is simply its utility. Moreover, if there is a choice, the MAX player should prefer the move leading to the state with the maximum value, and the MIN player - preferring to the state with the minimum value. Therefore, the following relationship holds.
 |
Apply these definitions to the game tree shown in the figure. Terminal nodes at the lowest level are already indicated by numbers that indicate their usefulness. The first MIN node, denoted as B, has three successors with values of 3, 12, and 8, so its minimax value is 3. Similarly, the other two MIN nodes have a minimax value of 2. The root node is the MAX node; his successors have minimax values of 3, 2, and 2, so the root node itself has a minimax value of 3. You can also define the concept of a minimax decision made at the root of the tree: action a 1 is the optimal choice for the player max, since it leads to the successor with the highest minimax value .
In this definition of the optimal game for the MAX player, it is assumed that the MIN player also plays in an optimal way: he maximizes the result corresponding to the worst outcome of the game for the MAX. What would happen if the MIN player did not play optimally? In this case, you can easily show that the player MAX would achieve even more. There may be other strategies of the game against opponents, playing in a non-optimal way, which allow to achieve more than the minimax strategy; but these strategies are necessarily worse against opponents who play optimally.
Minimax algorithm
The minimax algorithm calculates the minimax solution from the current state. It uses a simple recursive calculation of the minimax values of each successor state with the direct implementation of the governing equations. Recursion passes all levels up to the leaves of the tree, and then minimax values are reserved throughout the tree as the recursion is reversed.
For example, in the tree shown in the figure, the algorithm first performed a recursion with going down to the three lower left nodes and applied the utility utility function to them to determine that the utility values of these nodes are 3, 12, and 8, respectively. The algorithm then determines the minimum of these values, 3, and returns it as the reserved value of node B.
A similar process allows you to get the reserved values of 2 for node C and 2 for node D. Finally, take the maximum of the values 3, 2 and 2 to get the reserved value 3 of the root node.
 |
Comments
To leave a comment
Mathematical methods of research operations. The theory of games and schedules.
Terms: Mathematical methods of research operations. The theory of games and schedules.