Lecture
Separate fractal structures — the Cantor set, the Sierpinski carpet, a snowflake, etc. — are investigated. The concept of fractal dimension and the method of its calculation are introduced. The construction of the Mandelbrot set is described, and its analysis is carried out using a computer.
I. When order occurs in chaotic systems; the coexistence of chaos and order, the transition from one to another; competition or interoperability in complex systems is a common element - the competition of several centers for dominance on the plane or their interoperability. Usually, there is no simple structure of borders, more often there is a filigree interweaving and a struggle for their sections. In this border region, a transition occurs from one form of existence to another, from order to disorder and vice versa. Sometimes there is a third competitor who takes advantage of the differences of the other two and imposes his area of influence.
Ii. A mathematical approach to the description of such processes in nature was given in 1980 by the French mathematician Benoît Mandelbrot, who pointed out the fractal geometry of nature. Fractal objects are self-similar, that is, their appearance does not undergo significant changes when viewed in a microscope with any magnification. On sets having such a structure, it is said that they have geometric (scale) invariance. The processes generating such structures are feedback processes in which the same operation is performed again and again. Here, the result of one iteration is the initial condition for the next, and a nonlinear relationship between the result and the initial value is required, that is, the dynamic law x n + 1 = f (x n , C) is more complex than the linear x n + 1 = kx n .
Iii. There is an important quantitative characteristic of fractal objects - fractional dimension. Consider some set A and try to completely cover it with segments, squares or hypercubes with a side 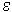 . Let N be the minimum number of cubes or squares needed to cover A. Consider the limit
. Let N be the minimum number of cubes or squares needed to cover A. Consider the limit
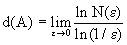 .
.
The value d (A) = dF is called the fractal dimension.
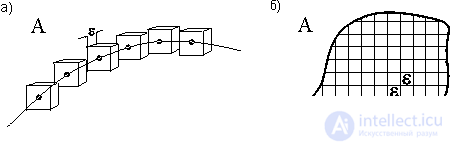
Fig. 1 Coating an object (set of points) with cubes with a long edge 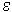 :
:
a) one-dimensional object, b) two-dimensional space.
As follows from this book, synergetics purposefully tries to find the rules by which order arises in chaotic systems; the coexistence of chaos and order, the transition from one to another; competition or interoperability in complex systems. These processes arise in various physical and mathematical problems. They have a common element: the competition of several centers for dominance on the plane or their mutual interaction. Usually, there is no simple structure of borders, more often there is a filigree interweaving and a struggle for their sections. In this border region, a transition occurs from one form of existence to another, from order to disorder and vice versa. Sometimes there is a third competitor who takes advantage of the differences of the other two and imposes his area of influence.
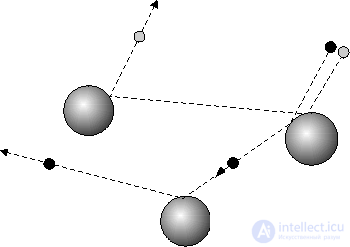
Figure 1. The movement of a small ball with randomly located large fixed balls .
It was noted above that any non-linear process leads to branching, to a fork in the path in which the system can choose one branch or another, but the consequences of the decision cannot be predicted. The smallest inaccuracies in the initial state of the system develop, at each particular moment the causal relationship remains, but after several branchings it is no longer visible. An example of such a system is given by the motion with the participation of hard balls, where the motion of a small ball colliding with large fixed balls randomly located in space (Fig. 1) is considered. If you make the slightest uncertainty in the initial conditions, then it will increase very quickly and makes it impossible to predict after the first few collisions about the location of small balls. Increasing the accuracy of the initial conditions will require an infinite increase in information, otherwise we will come to irreversibility.
These difficulties, as already noted, are characteristic not only of mechanical problems, they are also found in particle physics, in biology, and in sociology. New views in science, new concepts [15], new mathematical apparatus are required. This does not mean that the laws of nature known so far are wrong, simply we are not sufficiently aware of what is hidden in them. A mathematical approach to a broader view of nature was given in 1980 by the French mathematician Benoit Mandelbrot, who pointed to the fractal geometry of nature. The geometry we know is unable to describe the shape of a cloud, a mountain, a tree, or the seashore. In the above figure, the fractal structure of the blood vessels of the heart is clearly visible. Comparing the original image (top) and its enlarged fragment (below), you can be sure that the topology of large and small vessels is statistically identical.
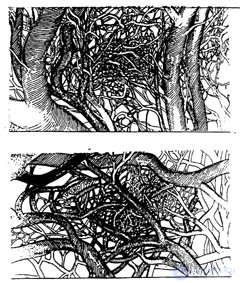
Nature shows us a completely different level of complexity associated with the amorphous morphology. Now we give the following fractals of "artificial origin":


Isn't it very plausible? The next example is already a scientifically significant result: on the left is a photograph of diffusion channels in a porous medium, and on the right is a mathematical fractal model of this process.
 |
 |
Fractal objects are self-similar, that is, their appearance does not undergo significant changes when viewed in a microscope with any magnification. On sets having such a structure, it is said that they have geometric (scale) invariance. The processes generating such structures are feedback processes in which the same operation is performed again and again.
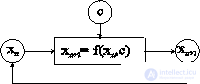
Fig. 2 Schematic diagram of the dynamic process xn + 1 = f ( xn , C)
Here, the result of one iteration is the initial condition for the next one (Fig. 2), and a non-linear relationship between the result and the initial value is required, i.e., the dynamic law x n + 1 = f (x n , C) is more complex than the linear x n +1 = kx n . As follows from fig. 2, the dependence x n + 1 on x n should contain the parameter C. If we start the iteration process with some value x 0 , then its result will be the sequence x 1 , x 2 , ... If we examine the behavior of such a sequence, we get (as rule) any fractal object. Such sequences are very different from ordinary sequences in mathematics. The next step depends on the previous and randomness, but not on the initial value. And in life most often it happens: your actions are mainly determined by the events of the previous days and partly by chance and do not depend on your birthday (do not touch astrology, because you can take any other day of your life for the initial value) .
Most of the examples of fractals in this paragraph are of “artificial” origin: i.e. self-similarity in them is a rule of construction. Through the paragraph, we will look at examples of fractals arising by the mechanism in Fig. 2, and then how the fractals are constructed and explored.
Comments
To leave a comment
Synergetics
Terms: Synergetics