19.4 Unsteady Poisson Flow

If the flow of events is non-stationary, then its main characteristic is instantaneous density. 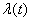. The instantaneous flux density is the limit of the ratio of the average number of events per elementary time interval. 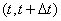, to the length of this section, when the latter tends to zero:

, (19.4.1)

Where 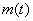- mathematical expectation of the number of events at the site .

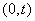Consider the flow of homogeneous events, ordinary and without aftereffect, but not stationary, with variable density 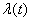. Such a stream is called a non-stationary Poisson stream. This is the first step of generalization compared to the simplest flow. It is easy to show a method similar to that used in 5.9, that for such a stream the number of events falling on the length segment 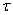starting at point 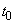obeys the Poisson law

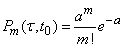
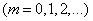, (19.4.2)

Where 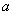- mathematical expectation of the number of events in the area from 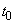before 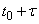equal to

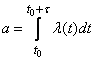. (19.4.3)

Here is the value 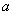depends not only on length 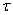plot, but also from its position on the axis .

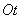We find for a nonstationary flow the distribution law of the time interval 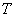between neighboring events. Due to the nonstationarity of the flow, this law will depend on where on the axis 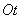The first event is located. In addition, it will depend on the type of function 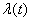. Suppose that the first of two adjacent events appeared at the moment 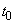and find under this condition the law of time distribution 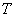between this event and the following:

.

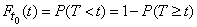We find - the probability that in the area from 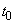before 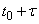no events will appear:

,

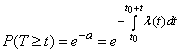from where

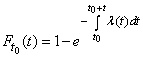. (19.4.4)

Differentiating, we find the distribution density

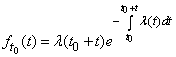
. (19.4.5)

This distribution law is no longer indicative. Its appearance depends on the parameter. 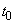and kind of function 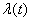. For example, with a linear change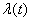

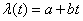
density (19.4.5) is

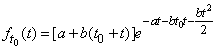. (19.4.6)

The schedule of this law is ; 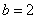and 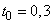presented in fig. 19.4.1.

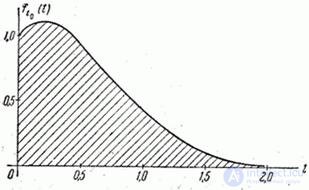
Fig. 19.4.1.

Despite the fact that the structure of a nonstationary Poisson flow is somewhat more complicated than the simplest one, it is very convenient in practical applications: the main property of the simplest flow — the absence of aftereffect — is preserved in it. Namely, if we fix on the axis 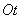arbitrary point 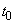then the distribution law 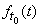of time 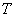, separating this point from the nearest future event, does not depend on what happened at the time interval preceding 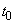and at the very point 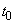(i.e., whether other events have appeared earlier and when).