Entropy of a continuous source of information

The entropy of a continuous source of information must be infinite, since the uncertainty of choice from an infinitely large number of possible states is infinitely great. (in fact, this is only an incorrect mathematical model, since real signals occupy a limited frequency spectrum, which means that they can be represented by discrete values ​​through a certain step determined by the Kotelnikov theorem ; in addition, real signals cannot be measured with infinite accuracy, since there are line noise and measurement error, which means that on the dynamic range scale, a continuous signal can also be represented by a finite number of distinguishable quantum levels - note by K.A. Khaidarov )

We divide the range of variation of a continuous random variable U into a finite number n of small intervals D u. When realizing the values ​​of u in the interval (u _n , u _n + D u), we will assume that the value u _{n of a} discrete random variable U 'has been realized, the probability of realization of which is:

p (u _n <u <u _n + D u) = 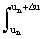p (u) du » p (u _n ) D u.

Entropy of discrete quantity U ':

H (U ') = - 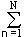p (u _n ) D u log (p (u _n ) D u).

Replace log (p (u _n ) D u) = log p (u _n ) + log D u, take into account that the sum p (u _n ) D u over all possible values ​​of u _n is equal to 1, and we get:

H (U ') = - 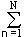p (u _n ) D u log p (u _n ) - log D u. (1.4.4)

In the limit, at D u ® 0, we obtain the expression for the entropy for a continuous source:

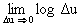H (U) = - p (u) log p (u) du - . (1.4.5)

The value of the entropy in (1.4.5), as expected, tends to infinity due to the second term of the expression. To obtain the final characteristics of the information properties of continuous signals, only the first term of expression (1.4.5) is used, which is called differential entropy . It can be interpreted as the average uncertainty in the choice of an arbitrary random variable compared with the average uncertainty in the choice of a random variable U ', which has a uniform distribution in the range (0-1). Indeed, for such a distribution p (u _n ) = 1 / N, D u = 1 / N, and for N ® Ґ it follows from (1.4.4):

H (U ') = - (log N) / N - log D u ® - .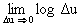

Accordingly, the difference in entropies gives the differential entropy:

h (U) = H (U) - H (U ') = - p (u) log p (u) du. (1.4.6)

The differential entropy does not depend on the specific values ​​of the quantity U:

h (U + a) = h (U), a = const,

but depends on the scale of its presentation:

h (kU) = h (U) + log k.

The practice of analyzing and processing signals usually deals with signals in a certain interval [a, b] of their values, while the maximum differential entropy has a uniform distribution of signal values:

h (U) = - 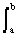p (u) log p (u) du = log (ba).

As the distribution density narrows, the value of h (U) decreases, and in the limit as p (u) ® d (uc), a <c <b, tends to zero.