Lecture
1. Entropy is a real and non-negative quantity, since the values of the probabilities p n are in the range 0-1, the values of log p n are always negative, and the values -p n log p n in (1.4.2) are respectively positive.
2. Entropy is a limited quantity, because for p n 10 0 the value -p n H log p n also tends to zero, and for 0 <p n Ј 1 the boundedness of the sum of all terms is obvious.
3. Entropy is equal to 0 if the probability of one of the states of the information source is equal to 1, and thus the state of the source is fully determined (the probabilities of the other states of the source are equal to zero, since the sum of the probabilities must be equal to 1).
4. The entropy is maximum at equal probability of all states of the information source:
H max (U) = - 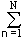 (1 / N) log (1 / N) = log N.
(1 / N) log (1 / N) = log N.
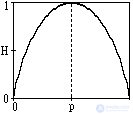
5. The entropy of a source with two states u 1 and u 2 with a change in the ratio of their probabilities p (u 1 ) = p and p (u 2 ) = 1-p is determined by the expression:
H (U) = - [p log p + (1-p) log (1-p)],
and varies from 0 to 1, reaching a maximum when the probabilities are equal. The graph of the entropy change is shown in Fig. 1.4.1.
6. The entropy of the combined statistically independent sources of information is equal to the sum of their entropies.
Let's consider this property on two sources of information u and v. When the sources are combined, we obtain a generalized source of information (u, v), which is described by the probabilities p (u n v m ) of all possible combinations of the states u n of the source u and v m of the source v. The entropy of the combined source for N possible source states u and M possible source states v:
H (UV) = - 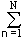
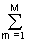 p (u n v m ) log p (u n v m ),
p (u n v m ) log p (u n v m ),
Sources are statistically independent from each other if the following condition is met:
p (u n v m ) = p (u n ) H p (v m ).
Using this condition, respectively, we have:
H (UV) = - 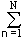
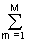 p (u n ) p (v m ) log [p (u n ) p (v m )] =
p (u n ) p (v m ) log [p (u n ) p (v m )] =
= - 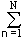 p (u n ) log p (u n )
p (u n ) log p (u n ) 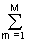 p (v m ) -
p (v m ) - 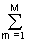 p (v m ) log p (v m )
p (v m ) log p (v m ) 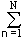 p (u m ).
p (u m ).
Taking into account that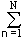 p (u n ) = 1 and
p (u n ) = 1 and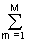 p (v m ) = 1, we get:
p (v m ) = 1, we get:
H (UV) = H (U) + H (V). (1.4.3)
7. Entropy characterizes the average uncertainty in the choice of one state from the ensemble, completely ignoring the content side of the ensemble. On the one hand, this expands the possibilities of using entropy in the analysis of a wide variety of phenomena, but, on the other hand, requires a certain additional assessment of emerging situations. As follows from Fig. 1.4.1, the entropy of states can be ambiguous, and if in any economic undertaking action u with probability p u = p leads to success, and action v with probability p v = 1-p leads to bankruptcy, then the choice of actions to estimate entropy may turn out to be the exact opposite, because the entropy for p v = p is equal to the entropy for p u = p.
Comments
To leave a comment
Signal and linear systems theory
Terms: Signal and linear systems theory