Lecture
Theme 6. The construction of codes given noise immunity. The use of non-binary error-correcting codes.
Lecture 9 .
Cyclic codes.
Recall once again about the encoding method in cyclic linear codes.
The formation of code words (coding) KC is performed by multiplying the information polynomial (the information polynomial is a polynomial with coefficients that are the information sequence) And i (X) of order i <k by the generating polynomial:
KS m + i (X) = g m (X) * AND i (X).
9.1 Matrix description of cyclic codes.
Cyclic codes can, like any linear codes, be described using matrices.
Recall that KC (X) = g m (X) * AND (X).
This corresponds to the simplified matrix multiplication method described above:
<! [if! vml]> 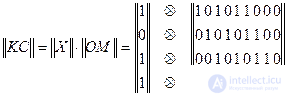 <! [endif]>
<! [endif]>
Forming matrix || OM || this (k * n) is the matrix with which the cyclic code is built. The generator matrix is obtained as a result of the k -multiple cyclic shift of the code combination corresponding to the first row of the generator matrix. The first row of the generator matrix is obtained by adding to the left of the coefficients of the polynomial g m (X) such number of zeros so that the total length of the code combination is n.
For example, the generator polynomial has the form G (X) = 111010001 = X 8 + X 7 + X 6 + X 4 +1 with n = 15 and k = 7. Then the first row of the generator matrix will look like: 000000111010001 , and the whole matrix:
0 0 0 0 0 1 1 1 1 0 1 0 0 0 1
0 0 0 0 0 1 1 1 0 1 0 0 0 1 0
0 0 0 0 1 1 1 0 1 0 0 0 1 0 0
0 0 0 1 1 1 0 1 0 0 0 1 0 0 0
0 0 1 1 1 0 1 0 0 0 1 0 0 0 0
0 1 1 1 0 1 0 0 0 1 0 0 0 0 0
1 1 1 0 1 0 0 0 1 0 0 0 0 0 0
Thus, it can be seen that, if we take the sets of the generating polynomial coefficients shifted to the right as the rows of the matrix generator, the calculation of code words using matrices is completely equivalent to the calculation of code words using polynomials.
9.2 Bose's codes - Chowdhury-Hokvingema (BCH).
Bose's codes - Chowdhury-Hokvingema (BCH) are a subclass of cyclic codes. Their distinctive feature is the ability to build a BCH code with a minimum distance d of not less than the specified one. This is important because, generally speaking, the construction of a Kodas with a distance of not less than a given one is a very difficult task.
In the BCH code, the generator of a polynomial is the product of several irreducible polynomials — we will see later what ones.
BCH codes, generally speaking, as well as linear cyclic codes in general, are not necessarily binary, that is, with the characters that make up the code = 1 or 0.
The characters of a CS word can be for example numbers of the form q m presented in the form of polynomials with non-binary coefficients. We consider binary codes, which allows us to avoid significant efforts to get acquainted with Galois field theory.
In BCH codes, the construction of the generating polynomial mainly depends on two parameters: on the length of the code word n = k + r and on the number of corrected errors S.
A feature of the code is that for correcting the number of errors S> = 2 there is still not enough condition that between code combinations there is a minimum code distance d min = 2 * S + 1 . It is also necessary for the code length n to satisfy the condition
n = 2 h - 1, (1)
where h is any integer.
In this case, the length of the code n will always be an odd number and take the values: 1,3,7,15,31,63,127..etc, that is, not all values of the length can be specified by the user.
The value n chosen by formula (1) determines the number of control characters r.
r <= h * s <= log 2 (n + 1) * s. (2)
When solving the problem of choosing the permissible number of information symbols for given corrective properties, it is convenient to use a table that contains correlations of corrective and information bits for BCH codes.
The construction of the generator polynomial G (X) is performed using the table of irreducible polynomials M (X). The generator polynomial is a product of irreducible polynomials and is their least common multiple (LCM). Maximum number of irreducible polynomial in their product
p = 2 * S - 1. (3)
The order of a polynomial is used in determining the number of factors. To construct G (X) , only odd polynomials are used.
For example, when S = 4, they will be: M1 (X); M3 (X); M5 (X); M7 (X). The oldest of them has the number p = 2 * S-1 = 7 . Their number is 4 , i.e. equal to the number of corrected errors.
The number of irreducible polynomials involved in the construction of the generator polynomial
V = S, (4)
a senior degree
v = h (5)
indicates a row in the table of irreducible polynomials, from which a polynomial is usually chosen to construct G (X). To construct the generating polynomial, only odd polynomials of degree v are used. Sometimes it is allowed to use polynomials and a lesser degree. The degree of the generating polynomial obtained by multiplying the selected irreducible polynomials,
b = r = v * s = h * s (6)
In general, G (X) = LCM [M1 (X) M3 (X) ... Mp (X)].
Example: Consider the construction of a 15- bit cyclic code that corrects one or two errors. According to (1),
n = 2 h - 1 , whence h = log 2 (n + 1) = log 2 16 = 4
The number of control characters k, according to (2),
r = log 2 (n + 1) * S = 4 * 2 = 8.
Number of the eldest of irreducible polynomials, according to (3)
p = 2 * S-1 = 2 * 2 -1 = 3.
The number of irreducible polynomials involved in constructing the generator polynomial, according to (4),
V = S = 2,
the highest degree, according to (5),
v = h = 4.
The degree of the generating polynomial, according to (6),
b = r = 8.
From the tables of irreducible polynomials we choose polynomials of degree v = 4 , from them we choose two (V = 2) irreducible polynomials, the number of the highest of which is 3 (p = 3), i.e. choose irreducible polynomials p1 and p3.
G (X) = M1 (X) * M3 (X) = 10011 * 11111 = 111010001 = X 8 + X 7 + X 6 + X 4 +1.
The number of information bits
k = n - m = 15 - 8 = 7.
The first line of the generator matrix is obtained by adding to the left of G (X ) such a number of zeros so that the total length of the code combination is equal to n. The generator matrix is obtained as a result of m times the cyclic shift of the code combination corresponding to the first row of the generator matrix.
0 0 0 0 0 1 1 1 1 0 1 0 0 0 1
0 0 0 0 0 1 1 1 0 1 0 0 0 1 0
0 0 0 0 1 1 1 0 1 0 0 0 1 0 0
|| OM || = 0 0 0 1 1 1 0 1 0 0 0 1 0 0 0
0 0 1 1 1 0 1 0 0 0 1 0 0 0 0
0 1 1 1 0 1 0 0 0 1 0 0 0 0 0
1 1 1 0 1 0 0 0 1 0 0 0 0 0 0
The remaining code combinations are obtained by multiplying 2 7 = 128 lines of different information words by the imaging matrix. Thus, we have obtained a set of code combinations for the above example consisting of 128 code words.
9.3 Systematic cyclic code view.
In practice, it is sometimes necessary to encode one or several information packages in the BCH code, for this we do as follows:
1) choose the generating polynomial (the method of selecting the generating polynomial is described above);
2) multiply the information combination by a monomial of the same degree as the polynomial that forms;
3) divide the resulting combination into a polynomial;
4) we add the remainder of the division with the information combination multiplied by the monomial of the same degree as the generator polynomial.
For example: the information combination of the type 1001101 is encoded in the BCH code, so that the code is able to correct errors of multiplicity 2 .
1. The seven-bit informational word and the correcting abilities of the code are 2 , therefore the polynomial chosen in the previous example is suitable for this case.
2. Multiply 1001101 by X 8 (100000000), we have 1001101 * 100000000 = 100110100000000
3. We divide 100110100000000 by 111010001 , by dividing modulo two, we get the remainder equal to 11000010
4. Summarize
100110100000000
+11000010
100110111000010 is the most sought- after combination.
Moreover, the older 7 bits are informational, and the remaining 8 are control ones.
Table 9.1 Decomposition of the binomial x n +1 into irreducible factors
Binomial degree | Sequences of root degrees of irreducible factors | Irreducible factors |
7 | 1 2 4 | 13 |
15 | 01 02 04 08 | 023 |
31 | 01 02 04 08 16 | 045 |
63 | 01 02 04 08 16 32 | 103 |
9.4 Reed – Solomon codes and their application.
A widely used subset of BCH codes are Reed-Solomon codes that allow you to correct error packets. The batch of errors of length b is a sequence of such b error symbols that the first and last of them are non-zero. There are classes of Reed-Solomon codes that allow for the correction of multiple error packets.
Reed-Solomon codes (RS) as binary elements ( 1 or 0 )) use binary vectors V with a length of 8 bits (bytes) or sometimes 4 bits (nibbles). RS codes, therefore, are not binary, as well as 8-mi RCH codes of length N = 2 m -1 .
They are cyclic polynomial codes.
G (x) = M1 (x) * M2 (x) * ... * Mi (X),
where the polynomial G (X ) before the powers of X i has a multiplier in the form of a binary vector 8 bits long.
The choice of the code length N = 2 m -1 ensures that the polynomial G (X) is a divisor of X N -1 , and therefore, the requirement for the generating polynomial of a cyclic code will always be fulfilled.
The code word Reed-Solomon has the form:
A 1 A 2 ... A k B 1 B 2 ... B Nk ,
where A i and B j are respectively informational and redundant symbols that can be represented by m- bit binary vectors. The number of information symbols is K = (N-Art. G (x)) , where Art. G (x) is the degree of the generating polynomial G (x) .
RS codes are systematic codes with a maximum code distance.
d = N-K + 1.
PC codes are linear codes, therefore, in addition to specifying using the generating polynomial G (X), they can also be specified by the generators || ОМ || by the matrix.
An example of an octal (7.3) Reed-Solomon code
Forming a polynomial in the Galois field GF (2 3 )
g ( x ) = x 4 + α 6 x 3 + α 6 x 2 + α 3 x + α,
where α is the first element of the Galois field GF (2 3 ). This is an octal or 3-digit binary number, such that α i run through all the values of the elements of the field GF (2 3 ) .
Let the source codeword consisting of octal numbers look like
IS = α 4 , α 0 , α 3 .
Forming polynomial, taken from the plate of primitive polynomials has the form
m ( x ) = α 4 x 2 + x + α 3
Reed-Solomon's code word will be written as
c ( x ) = m ( x ) g ( x ) = (α 4 x 2 + x + α 3 ) ( x 4 + α 6 x 3 + α 6 x 2 + α 3 x + α) = α 4 x 6 + α x 5 + α 6 x 4 + 0 x 3 + 0 x 2 + α 5 x + α 4 = (α 4 , α, α 6 , 0, 0, α 5 , α 4 )
what is a sequence of seven octal characters
Using Reed – Solomon Codes
Immediately after the appearance (the 60s of the 20th century), the Reed-Solomon codes began to be used as external satellite-satellite communications. Currently, Reed-Solomon codes have a very wide range of applications due to their ability to find and correct multiple error packets.
Recording and storage of information
The Reed-Solomon code is used when writing and reading in memory controllers, when archiving data, writing information to magnetic hard disks. Even if a significant amount of information is damaged, several sectors of disk media are corrupted, the Reed-Solomon codes allow recovering most of the lost information.
Reed-Solomon codes are widely used in digital audio recorders, including CDs. Data consisting of samples are combined into a frame representing the code word. Frames are divided into blocks of 8 bits. Part of the blocks are control.
Usually 1 frame (code word) = 32 blocks * 8 (data bits + signal bits + control bits) = 256 bits.
Signal symbols are auxiliary data that makes decoding easier: service signals, synchronization signals, etc.
When data is transmitted, interleaving (changing the order of the carrier along the time and in time) of blocks with different time shifts is performed, as a result of which dual errors are dissected, which facilitates their localization and correction. In this case, Reed-Solomon codes with irreducible code distance d 0 = 5 are used. This means that they are able to correct two byte errors in each code word of a frame of 256 bits.
9.5 Cyclic Redundancy CRC.
The CRC ( Cyclic Redundancy Check ) cyclic redundancy check is a systematic code designed not to correct errors, but to detect them. They use the systematic coding method outlined above: “checksum” is calculated by dividing x r u ( x ) by g ( x ) . Due to the fact that error correction is not required, verification of the correctness of the transfer can be done in the same way.
Thus, the type of the polynomial g ( x ) specifies a specific CRC code. These polynomials are standardized and have the following form. :
code name | power | polynomial |
CRC-12 | 12 | x 12 + x 11 + x 3 + x 2 + x + 1 |
CRC-16 | sixteen | x 16 + x 15 + x 2 + 1 |
CRC- CCITT | sixteen | x 16 + x 12 + x 5 + 1 |
CRC-32 | 32 | x 32 + x 26 + x 23 + x 22 + x 16 + x 12 + x 11 + x 10 + x 8 + x 7 + x 5 + x 4 + x 2 + x + 1 |
Table 9.2
9.6 Test questions.
1. How is the polynomial constructed to obtain the cyclic coding of the given noise immunity?
2. List the main steps in the construction of BCH codes.
3. Simplified coding method when encoding a single code word.
4. What is the peculiarity of the construction and application of Reed-Solomon codes,
bug fixes?
5. Is it possible to choose an arbitrary generator polynomial in CRC codes?
Comments
To leave a comment
Information and Coding Theory
Terms: Information and Coding Theory