Lecture
Lecture 8 .
8.1 Binary cyclic codes.
The above procedure for constructing a linear code using the matrix method has several disadvantages. It is ambiguous (MDR can be set in various ways) and inconvenient in implementation in the form of technical devices. These deficiencies lack linear correction codes belonging to the class of cyclic .
Cyclical call linear (n, k) -codes with the following property: for any codeword:
<! [if! vml]> 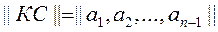 <! [endif]>
<! [endif]>
There is another code word:
<! [if! vml]> 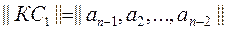 <! [endif]>
<! [endif]>
obtained by a cyclic shift of the elements of the source code word || Cop || right or left, which also belongs to this code.
For the description of cyclic codes use polynomials with dummy variable X.
For example, let the code word || Cop || = || 011010 ||.
It can be described by a polynomial.
<! [if! vml]> 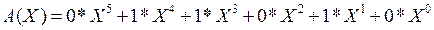 <! [endif]>
<! [endif]>
Thus, the bits of the code word in the polynomial describing it are used as coefficients with the degrees of the fictitious variable X.
The greatest degree of the dummy variable X in the term with a nonzero coefficient is called the degree of the polynomial. In the above example, a 4th degree polynomial is obtained.
Now actions on code words are reduced to actions on lines. Instead of matrix algebra, polynomial algebra is used here.
Consider the algebraic actions on polynomials used in the theory of cyclic codes. Summation of polynomials will be analyzed by the example of C (X) = A (X) + B (X).
Let be
|| A || = || 011010 ||, || In || = || 1101 11 |.
Then
<! [if! vml]> 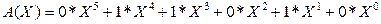 <! [endif]>
<! [endif]>
<! [if! vml]>  <! [endif]>
<! [endif]>
<! [if! vml]> 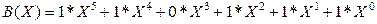 <! [endif]>
<! [endif]>
-------------------------------------------------- -------------
<! [if! vml]> 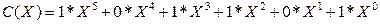 <! [endif]>
<! [endif]>
Thus, when summing the coefficients at X to the same degree, the result is taken modulo 2. With this rule, subtraction is equivalent to summation.
Multiplication is performed as usual, but using modulo 2 summation .
Consider multiplication by the example of multiplication of a polynomial (X 3 + X 1 + X 0 )
on the polynomial X 1 + X 0
X 3 + 0 * X 2 + X 1 + X 0
*
X 1 + X 0
-------------------------------------------------- -
X 3 + 0 * X 2 + X 1 + X 0
X 4 + 0 * X 3 + X 2 + X 1
____________________________________
X 4 + X 3 + X 2 + 0 * X 1 + X 0
The operation is the inverse of multiplication. Polynomials are divided as usual, except that subtraction is done modulo 2. Recall that subtraction modulo 2 is equivalent to addition modulo 2
Example of dividing the polynomial X 6 + X 4 + X 3 by the polynomial X 3 + X 2 +1
X 6 + 0 * X 5 + X 4 + X 3 + 0 * X 2 + 0 * X 1 +0 | X 3 + X 2 +1
X 6 + X 5 + 0 * X 4 + X 3 result == | X 3 + X 2
-----------------------------------
X 5 + X 4 + 0 * X 3 + 0 * X 2
X 5 + X 4 + 0 * X 3 + X 2
----------------------------------------
residual == X 2 = 100
The cyclic shift to the left by one position of the coefficients of a polynomial of degree n-1 is obtained by multiplying it by X and then subtracting from the result of the polynomial X n +1 if its order is > n.
Let's check it with an example.
Suppose you want to perform a cyclical shift to the left by one position
polynomial coefficients
C (X) = X 5 + X 3 + X 2 +1 → (101101)
The result should be a polynomial.
C 1 (X) = X 4 + X 3 + X 1 +1 → (011011)
This is easily proved:
C 1 (X) = C (X) * X- (X 6 +1) = (X 6 + X 4 + X 3 + X) + (X 6 +1) = X 4 + X 3 + X 1 +1
The cyclic code is based on a r- order generating polynomial (recall that r is the number of additional digits). We will denote it by g r (X).
The formation of code words (coding) of the CS is performed by multiplying the information polynomial with the coefficients, which are the information sequence I (X) of order i <k , forming the polynomial g r (X)
KS r + k (X) = g r (X) + IP k (X).
The received codeword may be different from the transmitted distorted bits as a result of interference.
PKS (X) = KS (X) + VO (X).
where VO (X) is the error vector polynomial, and summation, as usual, is carried out modulo 2 .
Decoding, as before, begins with finding the identification , in this case in the form of the OP (X) polynomial . This polynomial is calculated as the remainder of dividing the polynomial of the received PKS (X) code word by the generating polynomial g ( X):
<! [if! vml]>
 |
<! [endif]>
The first term has no remainder, since the code word was formed by multiplying the polynomial of the information sequence by the generator polynomial. Consequently, in this case the identifier is completely dependent on the error vector.
<! [if! vml]> 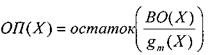 <! [endif]>
<! [endif]>
The generator polynomial is chosen such that, for a given r , the largest possible number of relations VO (X) / g (X) gives different residues .
This requirement is met by so-called irreducible polynomials that are not divisible by any polynomial of degree r and below, but are divided only by themselves and by 1.
The procedure for generating a code word given here is inconvenient because such code is obtained unsystematic, i.e. one in whose code words it is impossible to distinguish informational and additional digits.
This deficiency has been eliminated as follows.
The coding method, resulting in a systematic linear cyclic code, consists in assigning additional information bits to the information sequence AND AND .
These additional digits are proposed to be found by the following formula:
<! [if! vml]> 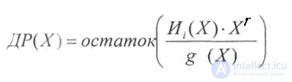 <! [endif]>
<! [endif]>
The order of the polynomial DR (X) is guaranteed to be less than r (since this is the remainder).
Attributing additional bits to the information sequence using algebra of polynomials can be described by the formula:
<! [if! vml]>
 |
<! [endif]>
One of the properties of cyclic linear codes is that the result of dividing any allowed code word by a CS into a generating polynomial is also a permitted code word.
Let us show that the code words obtained by the above algorithm are code words of a cyclic linear code. To do this, you need to make sure that an arbitrary resolved code word is divided into a generator polynomial g (X) without a remainder:
<! [if! vml]>
 |
<! [endif]>
Consider the first term:
<! [if! vml]> 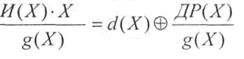 <! [endif]>
<! [endif]>
where d (X) is the integer part of the result of division.
Substitute the resulting amount in place of the first addend:
<! [if! vml]>
 |
<! [endif]>
Summation of the last two terms gives a zero result (recall that summation is performed modulo 2).
Means
<! [if! vml]>
 |
<! [endif]>
- the whole part of the division. No residue. This means that the encoding method described above corresponds to the cyclic code.
8.2 Some properties of cyclic codes.
All properties of cyclic codes are determined by the generator polynomial.
1. The cyclic code, which forms a polynomial containing more than one term, detects all single errors.
We will not strictly prove this. We show this by the example of the simplest generator polynomial g (X) = X + 1. The vector of a single error in the i -th digit is described by the polynomial BO (X) = X i .
<! [if! vml]>
 |
<! [endif]>
Find the identity
<! [if! vml]>  <! [endif]>
<! [endif]>
Thus, since VO has a weight of 1 (not zero), an error is detected.
2. It can be shown that the cyclic code formed with the help of the simplest primitive polynomial g (X) = X + 1 allows detecting not only single but also any errors of odd multiplicity. The proof is based on the fact that when using the generating polynomial X + 1 , the resulting code words necessarily have an even number of single digits.
Any distortion with an odd number of errors converts an allowed code word with an even number of units into a forbidden word with an odd number of units. Such a code word, since it is forbidden, will be immediately detected by the number of the remainder of its division by the forming polynomial.
We now find for the case of the generating polynomial X + 1 a simplified version of the encoding procedure.
Earlier, the following formula for obtaining a code word was given (the case of a systematic code):
<! [if! vml]>
 |
<! [endif]>
The remainder of dividing any polynomial by X + 1 can be either 0 ( no residual) or 1 . Consequently, r = 1 , that is, the generator polynomial X + 1 gives us one additional corrective discharge.
Considering the conclusion that when using the generating polynomial X + 1 , the resulting code words necessarily have an even number of single digits, we conclude that this one bit should complement the number of ones in the information part of the code up to an even number . This is a simplified coding method when using a separable cyclic code with the forming polynomial X + 1.
8.3 Methods for constructing cyclic codes
Cyclic codes can, like any linear codes, be described using matrices.
Recall that
<! [if! vml]>
 |
<! [endif]>
Let us also recall, using an example, the order of multiplication of polynomials:
<! [if! vml]>  <! [endif]>
<! [endif]>
This corresponds to the simplified matrix multiplication method described above :
<! [if! vml]>
 |
<! [endif]>
It can be seen that, if we take the sets of the generating polynomial coefficients shifted to the right as the rows of the generator matrix, the calculation of code words using matrices is completely equivalent to the calculation of code words using polynomials.
According to the second coding method, which allows to obtain a systematic code, the code word is found by the formula:
<! [if! vml]> 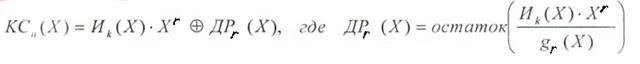 <! [endif]>
<! [endif]>
Forming matrix || OM || in this case it should consist of 2 parts - the unit matrix || I | | and matrices of additional digits || MDR ||, that is:
|| OM || = || I, MDR || .
The result of coding with the help of matrices will coincide with the result of coding with the help of polynomials in the event that the rows of the matrix of additional digits are formed by the following formula:
i- th line MDR = OST ((X i ) / g r (X)).
Further on the MDR, it is easy to construct a TBM to find identities and use the encoding- decoding procedures described above for linear codes .
8.4 Choosing a generator polynomial.
It is clear that the polynomials of the QS (X) code words must be divided into a polynomial of degree r without remainder . Cyclic codes are linear. This means that for these codes there are r linearly independent code words and with their help, by summation in different combinations, one can obtain all the other allowed code words of the given code. In order for all of them to be divided into a generator polynom without a remainder, it is sufficient that only r linearly independent codewords be divided into it without a remainder . These linearly independent codewords can be obtained by r -ting a cyclic shift to the right or left of any of the allowed codewords.
<! [if! vml]>
 |
<! [endif]>
Recall that a shift to the left corresponds to a multiplication of a codeword by X followed by subtraction, if, as a result of multiplication, a polynomial of order > n is obtained from the result of the polynomial X n +1. In a formula, the above can be displayed as follows.
where B = 1 if the degree g (X) * X i > = n
and where B = 0 if the degree g (X) * X i <n
The partial g i (X) / g (X ) has no remainder if the polynomial (X n +1) divides without remainder into the generator polynomial g (X) (obviously, the first term is divisible by g (X ) without remainder).
Thus, the generator polynomial g r (X) of a cyclic linear code must divide the polynomial X n +1 without a remainder .
This property ensures that there is no remainder when dividing the allowed code words by the forming polynomial. Such words 2 k . In total, there are different code words that can be obtained at the output of the communication channel 2 n . Among them, 2 r -1 prohibited, i.e. resulting from the distortion of the allowed codewords by interference. An error is detected if the remainder of their division by the generator polynomial is non-zero. The generator polynomial has order r. The maximum possible number of non-zero residues is 2 r -1. Only the so-called irreducible polynomials can give such a number of residues ; polynomials that are not divided without remainder into any polynomials other than 1 and themselves. A table of irreducible polynomials from 1 to 9 orders are given in the literature.
An example of a table of irreducible polynomials.
Table 8.1
Degree of polynomial | Polynomial | Binary word |
one | X + 1 | eleven |
2 | X 2 + x + 1 | 111 |
3 | X 3 + X + 1 | 1011 |
3 | X 3 + X 2 +1 | 1101 |
four | X 4 + X + 1 | 10011 |
four | X 4 + X 3 +1 | 11001 |
four | X 4 + X 3 + X 2 + X + 1 | 11111 |
9 | X 9 + X + 1 | 10000000001 |
| And another 40 pieces of polynomials |
|
8.5 Decoding cyclic codes
Error detection and correction occurs by the residuals from dividing the received combination F (X) by the generating polynomial G (X). If the accepted combination is divided into a generative polynom without a remainder, then the code is adopted correctly. The remainder of the division indicates an error, but does not indicate which one. To find the erroneous discharge and correct it in cyclic codes, it is customary to carry out the following procedures:
1) the accepted combination is divided into the forming polynomial;
2) the number of units in the remainder (remainder weight) is calculated. If W <= S, where S is the allowable number of errors corrected by this code, the adopted combination is added modulo 2 with the remainder. The amount will give the corrected combination. If W> S, then
3) produce a cyclic shift to the left of the received combination, divide the combination obtained as a result of the cyclic shift by the generating polynomial K (X). If the remainder W <= S, then add the dividend with the remainder. Then make a cyclic shift to the right of the resulting combination. The resulting combination no longer contains errors. If after the first cyclic shift and the subsequent division the remainder is obtained such that its weight W> S, then
4) the procedure of step 3 is repeated until W <= S. In this case
5) to make a cyclic shift to the right by as many digits as the combination that was summable with the last residue was shifted relative to the adopted combination. As a result, we get the corrected combination.
Example Show the process of correcting a single error in the received code combination.
Let there be a code word of the cyclic code 1001110, in which an error occurred in the fourth digit and the code 100 0 11 was received.
1. We divide the accepted combination into the generator polynomial g (X) = X 3 + X + 1
<! [if! vml]>  <! [endif]>
<! [endif]>
2. We compare the weight of the obtained residue W with the number of corrected errors S possible for a given code S. The number of corrected errors is S = 1 , i.e. W> S.
3. Perform a cyclic shift of the received combination F (X ) one digit to the left, followed by dividing the resulting cyclic shift of the combination by g (X):
4. We repeat the procedure until W <S
<! [if! vml]>
 |
<! [endif]>
5. Fold in modulo 2 the last dividend with the last remainder.
<! [if! vml]> 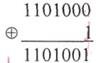 <! [endif]>
<! [endif]>
6. Perform a cyclic shift of the combination obtained as a result of summing the last dividend with the last remainder to the right by 4 digits (since before that we shifted the received combination to the left four times) 1110100, 0111010, 0011101, 1001110 as we see, the last combination corresponds to the transmitted one, t. E. No longer contains errors.
8.6 Test questions.
1. What section of mathematics is used in the construction of cyclic codes.
2. Basic honey badger for building a cyclic code.
3. What is the main feature of working with a polynomial representation of binary codes?
4. What are the basic requirements for generating polynomials?
5. What are the inconveniences of correcting errors in cyclic codes?
Comments
To leave a comment
Information and Coding Theory
Terms: Information and Coding Theory