Lecture
The convolution of functions is an operation in functional analysis.
By definition, a convolution is a mathematical operation applied to two functions f and g , generating a third function, which can sometimes be considered as a modified version of one of the original ones. Essentially, this is a special kind of integral transform.
The concept of convolution is generalized for functions defined on groups, as well as measures.
The convolution operation can be interpreted as the "similarity" of one function with a reflected and shifted copy of another.
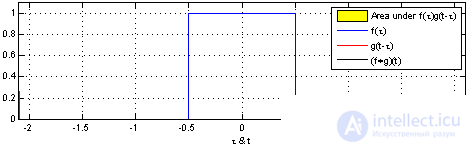
Convolution of two rectangular pulses: as a result gives a triangular pulse.
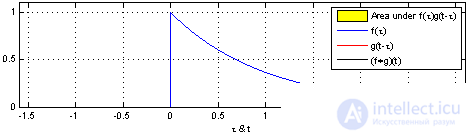
Convolution of a rectangular pulse (input signal) with an impulse response of an RC circuit
Let be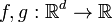 
- two functions that are integrable with respect to Lebesgue measure on the space 
. Then their convolution is called the function 
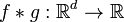defined by the formula
 |
 |
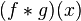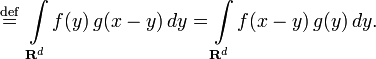In particular, when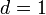 
the formula takes the form:
|
 |
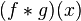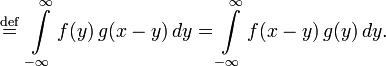Convolution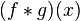 
determined for almost all 
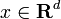and integrable.
For the first time, integrals that constitute a convolution of two functions are found in the writings of Leonhard Euler (1760s); later, the convolution appears in Laplace, Lacroix, Fourier, Cauchy, Poisson and other mathematicians. The designation of the convolution of functions using an asterisk was first proposed by Vito Volterra in 1912 in his lectures at the Sorbonne (published a year later) [1] .
.
.
.
,
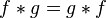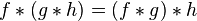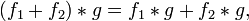
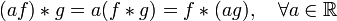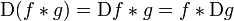Where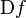 
denotes the derivative of the function 
on any variable.
,
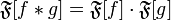Where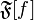 
denotes the Fourier transform of the function .
Let be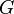 
- Lee group, equipped with a Haar measure 
and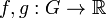 
- two functions defined on 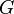. Then their convolution is called the function
.
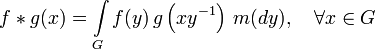Let there be a Borel space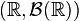 
and two measures 
. Then their convolution is called measure
,
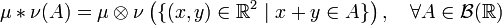Where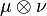 
denotes the product of measures 
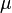and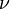 
.
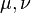absolutely continuous with respect to Lebesgue measure 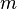. We denote their Radon-Nicodemus derivatives:
.
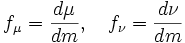Then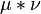 
also absolutely continuous regarding 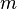and its derivative Radon - Nicodemus 
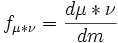has the appearance
.
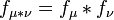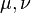- probability measures, then 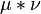also is a probabilistic measure.If a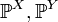 
- distribution of two independent random variables 
and 
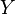then
,
Where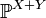 
- amount allocation 
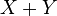. In particular, if 
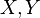absolutely continuous and have densities 
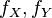, then a random variable 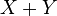also absolutely continuous and its density is:
.
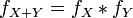Convolution of functions is the most important mathematical concept that is used in almost all areas of science and technology, including that it is widely used for evaluating image systems and for processing digital images. The convolution of two functions is a mathematical operation of two functions h (x) and f (x), generating the third function g (x), which can be considered as a modified version of one of the original ones, for example, after averaging or smoothing operations. The convolution h (x) and f (x) is written as h ∗ f (asterisk symbol). For continuous functions, it is defined as the integral of the product of two functions after one is reversed and shifted. Essentially, this is a special kind of integral transformation:
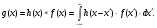(5.9)
The convolution operation is illustrated in Fig. 5.8 for two functions defined as rectangular pulses of different durations.
Fig. 5.8. An example of the convolution of two continuous functions h (x) and f (x). A darker color shows the area equal to the integral (5.9) for different values of x (adapted from [4])
The one-dimensional discrete convolution of two discrete functions h (i) and f (i) of length N is defined as
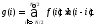(5.10)
From the point of view of the computational process, an easier and faster way to calculate the convolution of two functions is to use the convolution theorem. This theorem proves that the convolution of two functions is equivalent to the multiplication of their Fourier transforms in the frequency space. Thus, the convolution equation (5.9) can be expressed as
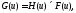(5.11)
where H (u) and F (u) is the Fourier transform of the functions h (x) and f (x) in the frequency space.
Comments
To leave a comment
Digital signal processing
Terms: Digital signal processing