Lecture
Definition 1 (main definition). Let X be an arbitrary set and t = { U } be a collection of its subsets with the following properties (topology axioms):
1) Æ , X Î t ;
2) the union of any collection of sets from t belongs to t ;
3) the intersection of any finite number of sets from t belongs to t .
Such a collection of subsets t is called a topology on X. A set X with a given topology t on it is called a topological space and is denoted by (X, t ), subsets from a collection of t are called open (in the space (X, t )).
Example 1 . X - number line R 1 . The topology on R 1 can be specified by the following set of subsets: the empty set Æ , all possible intervals and their unions U = . The topology axioms are easy to check. 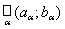
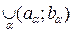
Example 2. X = R 2 . An open set is any set in X = R 2 that, together with each of its points, contains a sufficiently small open circle centered at this point, as well as an empty set. This definition is consistent with the standard understanding of open sets given in the Mathematical Analysis course. It is easy to check that the system of all open sets in X = R 2 forms a topology.
Example 3 . X is an arbitrary set. The collection t min = { Æ , X} obviously defines a topology on X. Thus, the defined topology on X is called minimal or trivial.
Example 4 . X is an arbitrary set, t max = {all possible subsets of X}. The collection t is a topology on X. This topology is called maximal or discrete .
Thus, on the same set, one can introduce different topologies, for example, trivial and discrete.
Closely related to the concept of an open set in a topological space (X, t ) is the dual concept of a closed set : this is the name of a set whose complement to X is open. In other words, if U Î t , then X \ U is closed, and vice versa: if F is closed, then X \ F is open.
Due to the dual nature of operations in set theory, the collection {F} of all closed sets of a topological space (X, t ) satisfies the following properties:
1) X, Æ Î {F};
2) the intersection of any collection of sets from {F} belongs to { F };
3) the union of any finite number of sets from {F} belongs to { F }.
These properties completely characterize the closed sets of the topological space (X, t ), and, consequently, the topology of t (since sets from t are complements of closed sets) and can be taken as the axioms of the topological space. Thus, a topology on X can be specified by specifying a collection { F } of subsets of X satisfying properties 1) - 3); in this case, the topology on X is the collection { X \ F }.
Different topologies on the same set form a partially ordered set.
Definition 2. The topology of t on X is said to be weaker than the topology t 'on X ( t £ t ') if from the fact that U Î t it follows that U Î t ', that is, if t Ì t '. The topology t 'in this case is stronger than the topology t .
Note that for any topology t we have t min £ t £ t max .
It is very often difficult to obtain a description of the entire topology as a collection of some subsets of X. To define the topology, the construction of a set of subsets that generate the topology is used.
Definition 3. The set  = {V} topological open sets of (x, t ) is called a base topology t , if for each open set U Î t and for each point x Î U there is a plurality of V Î Â , that x Î V and the V Ì the U .
Consequently, any non-empty open set of a topological space (X, t ) can be represented as a union of open sets from the base of the topology t (this property characterizes the base and is often taken as the definition of the base). It is enough to take the union of all open sets from the base that are embedded in this set.
Let {V a } be some collection of subsets of X. The question arises: under what conditions can a topology on X be constructed so that the family {V a } is the base of this topology?
Theorem 1 (base criterion ). Let {V a } a Î A be some non-empty collection of subsets of X. Then J = {V a } a Î A is a base of some topology on X if
1) X = , 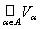
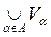
2) for each V a and each V b from J and each x Î V a Ç V b, there exists V g Î Â such that x Î V g Ì V a Ç V b .
Evidence. If  = {V a } a Î A - topology database, then V a Į V b - open set, and to determine the base for each x Î V a Į V b exists V g Î Â such that x Î V g Ì V a Ç V b .
Conversely: if  = {V a } a ΠA satisfies the condition of the theorem. We say that a set U Πt if U = V 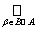
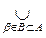 b . The membership of X Î t follows from condition 1). The membership of Æ Î t is a consequence of the multiple equality V b = Æ . The second axiom is verified directly:, i.e. the union of sets from t can be represented as the union of sets from В and, therefore, also belongs to t
b . The membership of X Î t follows from condition 1). The membership of Æ Î t is a consequence of the multiple equality V b = Æ . The second axiom is verified directly:, i.e. the union of sets from t can be represented as the union of sets from В and, therefore, also belongs to t 
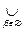
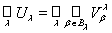
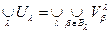 ... Let us check the third axiom. To do this, take arbitrary two sets U 1 , U 2 Î t . According to the definition of the system t , the representations U 1 = V b , U 2 = V d are valid . Then
... Let us check the third axiom. To do this, take arbitrary two sets U 1 , U 2 Î t . According to the definition of the system t , the representations U 1 = V b , U 2 = V d are valid . Then 
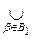

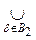
U 1 Ç U 2 = ( V 
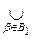 b ) Ç ( V
b ) Ç ( V 
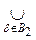 d ) = (V
d ) = (V 
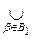

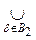 b Ç V d ).
b Ç V d ).
For the proof it is sufficient to show that the V b Į the V d = , where 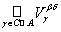
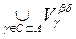
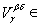
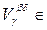 Â . Then U 1 Ç U 2 = , that is, the union of sets from
 . Then U 1 Ç U 2 = , that is, the union of sets from 
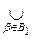

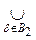
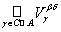
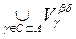 J , and hence U 1 Ç U 2 from t . As a system of sets in the equality being proved, we take all sets from
J , and hence U 1 Ç U 2 from t . As a system of sets in the equality being proved, we take all sets from 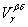
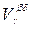 J satisfying the condition
J satisfying the condition 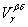
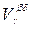 Ì V b Ç V d . Then the inclusion
Ì V b Ç V d . Then the inclusion 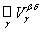
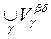 Ì V b Ç V dobvious. Let us prove the reverse inclusion. Take an arbitrary x Î V b Ç V d . By the definition of system J, there is a
Ì V b Ç V dobvious. Let us prove the reverse inclusion. Take an arbitrary x Î V b Ç V d . By the definition of system J, there is a 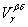
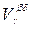 Î J such that x Î Ì V b Ç V d . This means that x Î and the inclusion V a b Ç V a d Ì is valid .
Î J such that x Î Ì V b Ç V d . This means that x Î and the inclusion V a b Ç V a d Ì is valid . 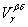
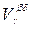
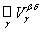
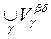
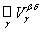
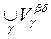
Note that in the proof we also indicated a method for constructing the topology if a family  = {V a } a ΠA is given that satisfies the conditions of the theorem.
EXAMPLE 5 n ust X = R n e nce n -dimensional in Vectorial space. In as b ase m opologii n and R n m You can a son with istemu m nozhestv  = V { a , b } , r de V a , b = {x Î R n : and i < x i < b i , i = 1 , . .., n } , x i - coordinate in the vector x = ( x 1 , x 2 ,…, x n ) ; а = ( а 1 , a 2 , ..., а n ) , b = ( b 1 , b 2 , ..., b n ) - p roizvolnye in projectors in R n , n Rich and i < b i .
Such m nozhestva V a , b n indicates the card about Access the parallelepipeds in R n .
The d -trivial, if N e b udet have seemed to Which and Menno topology p assmatrivaetsya n and R n , m s b Udem with read h then R n is provided topologist iey, b ase to otorrhea have proved to claim Reamer 5.
In topological n a space of e stestvenno in ybirat b ase poplar ogii with a POSSIBILITY m enshim to The number e lementov. For example, in R 1 m nozhestva V = ( t 1 , t 2 ), g de t 1 , t 2 p ational numbers form b ase top ologii and h with even hours Isla e lementov.
Comments
To leave a comment
Functional analysis
Terms: Functional analysis