Lecture
N ust ( x, t ) - a topological space and x Î X - arbitrary m points.
DEFINITION 4. On the vicinity of xS m points x Î X n be ordered every n odmnozhestvo U ( x ) Ì x , y dovletvoryayuschee in words:
1 ) x Î U ( x );
2 ) with uschestvuet V Î t t Which, h then x Î V Ì U ( x ).
Note that by virtue of this definition, any open set is a neighborhood of each of its points. The neighborhood of a point that is an open set is called an open neighborhood .
You can p assmatrivat with ovokupnost in seh about the vicinity of xS this t points x . E that with ovokupnost of bladaet with leduyuschimi properties (prove it!):
1) in syakoe m nozhestvo, to win a Mr. ome neighborhood so points x , I S THE about the vicinity of xS t points x ;
2) n eresechenie to f course hours Isla about the vicinity of xS m points x - neighborhood of the hibernation x ;
3) about bedinenie either with ovokupnosti about the vicinity of xS point x ec five neighborhood t achki x .
Theorem 2. P odmnozhestvo A (A ¹ Æ ) topological space ( x, t ) of eopen t hen and t nly t hen when about but sod erzhit N ome of the vicinity of xS to azhdoy its t glasses.
Evidence. P Ust And about eopen, x Î A . T hen I understood that the A - about the vicinity of xS x , with been consistent, And to win a neighborhood l Juba with voey t glasses.
N ust d la to azhdogo x Î A exists on the vicinity of xS U m points x , y Elika l ezhaschaya in A: U Ì A . N of the definition of the vicinity of xS in n s with possessed N ome open m nozhestvo V x , x Î V x Ì U Ì A . Russ Motril on bedinenie in 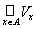
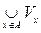 cex so Akiha m nozhestv. Oh but of eopen and coincides with A . D Valid The, t ak to ak in syakaya m points of the set A n rinadlezhit , m of A Ì . C d nother hand, to azhdogo x and Lev Mey V x Ì A , m .
cex so Akiha m nozhestv. Oh but of eopen and coincides with A . D Valid The, t ak to ak in syakaya m points of the set A n rinadlezhit , m of A Ì . C d nother hand, to azhdogo x and Lev Mey V x Ì A , m . 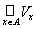
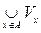
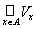
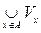 e .
e . 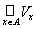
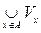 Ì A . P oetomu A = s nachit, A to Access the.
Ì A . P oetomu A = s nachit, A to Access the. 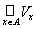
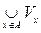
Theorem 3. A set A Ì R 1 is open if and only if it can be represented in the form (recall that the sum of sets is understood as their union, provided that these sets do not intersect with each other). 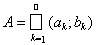
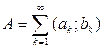
Evidence. The sufficiency of the statement is obvious; let us establish the necessity. On the set A, we introduce the relation x ~ y if there exists an interval ( a ; b ) Ì A containing both of these points. This relationship is an equivalence. The first two conditions in the definition of equivalence are easy to check. The latter implies that if two intervals belong to A and have a common point, then their union will also be an interval, and belonging to A.
As a result, the set A is divided by this equivalence relation into disjoint equivalence classes. Consider one such class [ x ] and let and . Since the set A is open, then any point of this set is internal, i.e. enters A with some interval. Therefore, always 
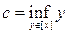
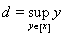
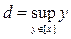 c < d . It may happen that these numbers are infinity. In this case, the reasoning is simpler. Let - ¥ < c < d <+ ¥ . We show that ( c ; d ) Ì A . Indeed, let s Î ( c ; d ). Due to the properties of exact faces and number sets, there are y and z from [ x ] such that c < y < s < z < d . Since y ~ z , there exists an interval ( r ; q ) Ì A and such that y , z Î ( r ; q ). But then s Î ( r ; q ) Ì А and this proves that ( c ; d ) Ì A . Note that at the same time we have practically shown that s Î [ x ] belongs . This means that ( c ; d ) Ì [ x ]. Since the reverse embedding is obvious from the definitions of c and d , then [ x ] = ( c ; d ).
c < d . It may happen that these numbers are infinity. In this case, the reasoning is simpler. Let - ¥ < c < d <+ ¥ . We show that ( c ; d ) Ì A . Indeed, let s Î ( c ; d ). Due to the properties of exact faces and number sets, there are y and z from [ x ] such that c < y < s < z < d . Since y ~ z , there exists an interval ( r ; q ) Ì A and such that y , z Î ( r ; q ). But then s Î ( r ; q ) Ì А and this proves that ( c ; d ) Ì A . Note that at the same time we have practically shown that s Î [ x ] belongs . This means that ( c ; d ) Ì [ x ]. Since the reverse embedding is obvious from the definitions of c and d , then [ x ] = ( c ; d ).
The last equality completes the proof of the theorem, since there cannot be more than a countable number of such intervals contained in A. Indeed, in each interval it is sufficient to take a rational number. Different numbers will correspond to different intervals, and the number of intervals is bijectively mapped into a subset of the set of rational numbers. The latter, as a subset of a countable set, must be at most countable.
Consequence. Any closed set on the line is obtained from the line by discarding a finite or countable number of intervals.
Neighborhood and Use for about tdeleniya t ochek e pyr of t other.
5. Determination of topological n a space of ( X, t ) is called the Hausdorff or separable , e fusion d la l yubyh two e of different m ochek, x , y , n aydutsya t Which of the vicinity of xS V ( x ), V ( y ) e silent t ochek, h the V ( x ) Ç V ( y ) = Æ .
Topological n a space of ( x, t ) with t rivialnoy topology not I S THE Hausdorff, ie If it is about to win more on the ne t glasses ( check!).
Properties of the vicinity of xS t glasses, p assmotrennye in yshe can pos it in on again with leduyuschego of EFINITIONS topological space consisting of TBA, about byavlyaya and x and ksiomami.
Definition 6 . The topological space - e the sets of X , d la to azhdoy m points x to otorrhea have proved nonempty with YSTEM submanifold nozhestv {O ( x )} n be ordered neighborhoods m points x , Satisfactory oryayuschih with leduyuschim properties:
1 ) x belongs to each with a howl about the godhood O ( x );
2 ) e fusion m nozhestvo U Ì X with win n ome O ( x ), the U - m akzhe about the vicinity of xS m points x ;
3 ) d A l yubyh neighborhoods Tei O 1 ( x ), O 2 ( x ) m points x and x n eresechenie O 1 ( x ) Į O 2 ( x ) t akzhe I S THE about the vicinity of xS m points x ;
4 ) d To a sjakoj neighborhood of O ( x ) m points x n EIDET t Which of the vicinity of xS O 1 ( x ) Ì O ( x ) to the otorrhea is tsya about the vicinity of xS to azhdoy with voey point.
Comments
To leave a comment
Functional analysis
Terms: Functional analysis