Lecture
Definition 7 . A metric space is a pair (X, d), where X is an arbitrary set, and d: X ´ X ® R is a mapping, called a metric , satisfies the following three axioms:
1. d ( x , y ) ³ 0; d ( x , y ) = 0 Û x = y (non-negativity).
2. d ( x , y ) = d ( y , x ) (symmetry).
3.d (x, y) £ d (x, z) + d (z, y) (triangle inequality ).
Example 6. Euclidean space R n consists of the set of all n -dimensional vectors, the metric in which is given by the equality d (x, y) = . The validity of the metric axioms (with the exception of the triangle inequality) is obvious. The triangle inequality follows from the Minkowski inequality for sums (see Appendix). The metric introduced in this way on R n is called Euclidean . 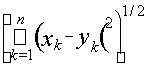
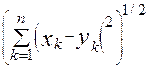
Example 7. In the space of continuous functions C [ a , b ] on the segment [ a , b ], we introduce the metric d (x, y) = max | x (t) - y (t) |, where the maximum is taken over t Î [ a , b ]. This metric is called the Chebyshev metric . The validity of the metric axioms is almost obvious.
Example 8. С k [a, b] is the metric space of all continuous functions on [a, b], having continuous derivatives up to order k, with the metric defined by the formula
d (x, y) = . 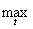
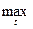
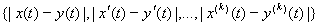
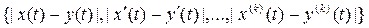
The validity of the metric axioms is obvious.
Example 9. M [a, b] is the space of bounded real functions x (t) defined on the segment [a, b] with metric d ( x , y ) = . It is clear 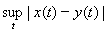
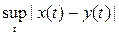 that C [ a , b ] Ì M [ a , b ]. The validity of the metric axioms is obvious.
that C [ a , b ] Ì M [ a , b ]. The validity of the metric axioms is obvious.
Example 10. l p (1 £ p < ¥ ) is the space of all numerical sequences x = { x k } for which the series converges . The metric in this case is defined as follows: 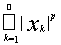
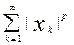
d ( x , y ) = < 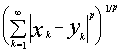
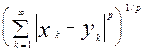 ¥ .
¥ .
The fulfillment of the first two axioms is obvious. The triangle inequality follows from the Minkowski inequality (see the appendix).
Example 11. l ¥ = m is the space of bounded number sequences with metric
d (x, y) = sup | x k - y k |
The validity of the metric axioms is obvious.
Example 12. with 0 is the space of sequences converging to zero with the same metric as in m .
Example 13. For an arbitrary set X, define the metric
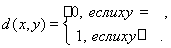
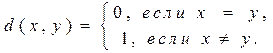
The validity of the metric axioms is obvious. The considered space is called a discrete metric space.
Example 14. s is the space of all numerical sequences . We introduce a metric into s by the relation:

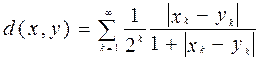
Axioms 1 and 2 of the metric are obvious, the fulfillment of axiom 3 follows from the increase in the function t / (1 + t) (check!).
Definition 8 . We denote by S ( x 0 , r ) = { x : d ( x 0 , x ) < r } is an open ball , S [ x 0 , r ] = { x : d ( x 0 , x ) £ r } is a closed ball .
Example 15 . Let X = R 3 be a three-dimensional Euclidean space. The ball S (a, r) is an ordinary ball of radius r centered at a = (a 1 , a 2 , a 3 ).
|
Example 16. Let X = C [a, b ], then the ball (a, r) in the space C [a, Definition 9 (topology of a metric space ). We define the base of the topology J in the metric space ( X , d ) assuming that J = { S ( x , r ): " r > 0, " x Î X }. Obviously, this family satisfies the conditions of Theorem 1 and generates a topology in a metric space. |
|
Note the following property of distances, which can be called the “ quadrilateral inequality ”: for any four points x, y, z, u of the metric space
| d (x, y) - d (z, u) | £ d (x, z) + d (y, u).
Geometrically, this means that the difference between the two sides of the quadrilateral does not exceed the sum of the other two sides.
The proof follows from the inequalities
d (x, y) £ d (x, z) + d (z, u) + d (u, y),
d (z, u) £ d (z, x) + d (x, y) + d (y, u),
if d (z, u) is subtracted from the first , and d (x, y) from the second . For y = u , the quadrilateral inequality turns into the second triangle inequality
| d (x, y) - d (y, z) | £ d (x, z ),
which is also often used.
Comments
To leave a comment
Functional analysis
Terms: Functional analysis