3.3. The definite integral and its applications 3.3.1. The concept of a definite integral

The function f ( x ) is defined on the interval [ a; b ] . Inside the segment, take n consecutive points x 1 , x 2 ,. . . x n (Fig. 12).

Fig. 12

Denote by a = x o , b = x n + 1 . The whole segment is divided into ( n + 1) partial intervals. In each interval, take the point

Find the function values 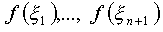and the lengths of the intervals h 1 = x 1 - x o , ..., h n + 1 = x n + 1 - x n .

Make up the amount 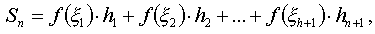which is called the integral sum . Let h be the length of the longest interval, i.e. h = maxh i . Let n tend to infinity so that h tends to zero.

The final limit of the sequence S n (if it exists) as h → 0 , which does not depend on the method of dividing the segment [ a, b ] into n + 1 intervals, nor on the choice of points ξ 1 , ..., ξ n + 1 , is called a definite integral of the function f ( x ) on the interval [ a, b ] and is denoted by 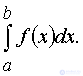The function f ( x ) is called an integrable function, the number a is called the lower limit of integration , the number b is called the upper limit of integration , the segment [ a, b ] is the segment of integration .

A continuous function on the interval [ a, b ] is an integrable function on [ a, b ] .