Integrals. History reference. The use of integrals in practice

There are several types of integrals: indefinite and definite integrals, the Riemann and Riemann – Stieltjes integrals, Lebesgue and Lebesgue – Stieltjes integrals, Daniel integrals. According to the area of ​​integration, the integrals are divided into multiple, curvilinear and surface integrals. Integral is one of the most important concepts of mathematical analysis that occurs when solving problems of finding the area under a curve, the path traveled with uneven movement, the mass of a heterogeneous body, and the like, as well as in the problem of restoring a function from its derivative ( indefinite integral ). The integral can be simplified as an analogue of the sum for an infinite number of infinitely small terms.

History reference

The basic concepts of integral calculus introduced in the works of Newton and Leibniz at the end of the XVII century. Leibniz belongs to the designation of the integral 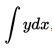reminiscent of the integral sum, like the symbol itself 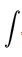from the letter 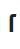("Long s") - the first letter in the Latin word summa (then umma , sum) [1]. The term “integral” was proposed by Johann Bernoulli, a student of Leibniz. The designation of the limits of integration in the form 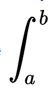introduced by Fourier in 1820.

A rigorous definition of the integral for the case of continuous functions was formulated by Cauchy in 1823, and for arbitrary functions by Riemann in 1853. The definition of the integral in the sense of Lebesgue was first given by Lebesgue in 1902 (for the case of a function of one variable and Lebesgue measure).

Integration dates back to ancient Egypt from about 1800 BC. e., as evidenced by the Moscow Mathematical Papyrus (or the Mathematical Papyrus Golenishcheva). The first known method for calculating integrals is the method for studying the area or volume of curvilinear figures - the method of exhausting Eudox (Evdoks of Cnidus (c. 408 BC - c. 355 BC) - the ancient Greek mathematician, mechanic and astronomer), which was proposed in about 370 BC. er The essence of this method is as follows: the figure, the area or volume of which they were trying to find, was divided into an infinite number of parts for which the area or volume is already known. This method was further developed in the works of ancient Greek mathematician, physicist and engineer Archimedes (287 BC - 212 BC) for calculating the areas of parabolas and an approximate calculation of the area of ​​a circle. Similar methods were developed in China in the third century AD by the Chinese mathematician Liu Hui (c. 220 - c. 280), who with their help found the area of ​​a circle. To find the volume of the ball, this method was used by a Chinese mathematician, astronomer, mechanic, writer Zu Chunzhi (429-500) together with his son, also a mathematician and astronomer, the governor of the region and the state treasurer, Zu Geng.

Further, a big step forward in the development of integral calculus was undertaken in Iraq in the 11th century by an Arab universal scientist, mathematician, mechanic, physicist and astronomer Abu Ali al-Hassan ibn al-Hassan ibn al-Haysam al-Basri (965-1039) (or Ibn al-Haysam, in Europe known as Alhazen), who in his work "On the measurement of a parabolic body" gives formulas for the sum of consecutive squares, cubes and fourth degrees, and a number of other formulas for the sums of rows. With the help of these formulas, he carries out the calculation, equivalent to the calculation of a definite integral:

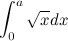
Using mathematical induction, he was able to generalize his results for integrals from polynomials to fourth degree. Thus, he was close to finding a general formula for integrals of polynomials of no higher than fourth degree.

The next significant push in calculating integrals took place only in the 16th century in the works of the Italian mathematician Bonaventure Francesco Cavalieri (1598 - 1647), which described the method of indivisible proposed by him, as well as in the works of the French mathematician Pierre de Fermat (1601 - 1665). These scholars laid the foundations of modern integral calculus. Further development is connected with the activities of the English mathematician, physicist and theologian Isaac Barrow (1630 - 1677) and the Italian mathematician and physicist, student of Galileo Evangelista Torricelli (1608 - 1647), who presented the first hints on the connection between integration and differentiation.

During the formation of integral calculus, the designation of the integral also changed. The English physicist, mechanic, mathematician and astronomer Isaac Newton (1643 - 1727) used, though not in all his works, the square icon in front of or behind the function as well as the vertical line above the function as an integration symbol, but these symbols did not get wide distribution. The modern designation of the indefinite integral was introduced by the German philosopher, logician, mathematician, mechanic, physicist, lawyer, historian, diplomat, inventor and linguist Gottfried Wilhelm Leibnitz (1646 - 1716) in 1675. He formed the integral symbol of the letter "long s" (from the first letter of the word Summa - sum) The modern designation of a definite integral, indicating the limits of integration, was first proposed by the French mathematician and physicist Jean Baptiste Joseph Fourier (1768 - 1830) in 1819-20 . The term "integral" was coined by the Swiss mathematician Jacob Bernoulli (1654 - 1705) in 1690.

The use of integrals in practice

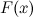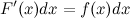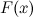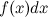The main task of differential calculus is to determine for a given function its derivative or its differential . The inverse problem of defining the function by its known derivative or differential , is the main task of integral calculus.

Application of a definite integral to amatics

1. Calculate the area of ​​a flat figure in rectangular coordinates.
2. Calculation of the area of ​​a flat figure in polar coordinates.
3. Calculate the volume of the body of revolution.
4. Calculate the arc length of a curve.
5. Calculation of the surface area of ​​the body of revolution. etc.

Application of a definite integral in physics

1. Work A is a variable force.
2. S - (path) movement passed by the body.
3. Mass calculation
4. Calculation of the moment of inertia of the line, circle, cylinder.
5. Calculation of the center of gravity.
6. Quantity of heat
7. Fluid pressure on vertical plate, etc.

Application of a definite integral in biology

1. Population size.
2. Biomass population.
3. The average length of the span (mileage) of an animal, etc.

Application of a definite integral in the economy

1. discounted cash flow value
2. cost function definition
3. material cost forecasting
4. finding consumer surplus
5. determination of the volume of output,
6. determination of the economic efficiency of capital investments (the problem of discounting), etc.