Lecture
A stochastic process (probabilistic process, random function, stochastic process) in the theory of probability is a family of random variables indexed by some parameter, most often playing the role of time or coordinates.
Other definition:
Random process is u (t), the instantaneous values of which are random variables.
Let probabilistic space be given 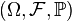 . Parameterized family
. Parameterized family  random variables
random variables
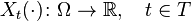 ,
,
Where  An arbitrary set is called a random function.
An arbitrary set is called a random function.
 then parameter
then parameter 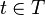 can be interpreted as time. Then a random function
can be interpreted as time. Then a random function 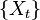 called a random process. If many
called a random process. If many 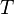 discretely for example
discretely for example 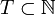 then such a random process is called a random succession .
then such a random process is called a random succession . where
where 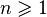 then parameter
then parameter 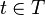 can be interpreted as a point in space, and then the random function is called a random field .
can be interpreted as a point in space, and then the random function is called a random field .This classification is not strict. In particular, the term “random process” is often used as an unconditional synonym for the term “random function”.
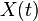 called a process discrete in time , if the system in which it flows, changes its state only at times
called a process discrete in time , if the system in which it flows, changes its state only at times 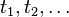 whose number is finite or countable. A random process is called a process with continuous time , if the transition from state to state can occur at any time.
whose number is finite or countable. A random process is called a process with continuous time , if the transition from state to state can occur at any time.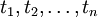 but not from the actual values of these quantities. In other words, a random process is called stationary if its probabilistic laws are constant in time. Otherwise, it is called non-stationary .
but not from the actual values of these quantities. In other words, a random process is called stationary if its probabilistic laws are constant in time. Otherwise, it is called non-stationary .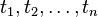 where
where 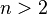 , but
, but 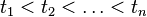 random variables
random variables  ,
, 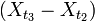 ,
, 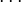 ,
, 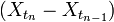 independent in the aggregate.
independent in the aggregate.Let a random process be given.  . Then for each fixed
. Then for each fixed 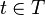
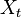 - a random variable called a section . If fixed elementary outcome
- a random variable called a section . If fixed elementary outcome 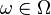 then
then 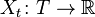 - deterministic parameter function
- deterministic parameter function 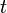 . Such a function is called a trajectory or a realization of a random function.
. Such a function is called a trajectory or a realization of a random function. 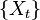 .
.
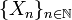 where
where 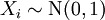 is called the standard Gaussian (normal) random sequence.
is called the standard Gaussian (normal) random sequence.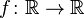 and
and  - random value. Then
- random value. Then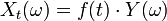
is a random process.
A function X (t) is called random if its value for any argument t is a random variable. Random functions of time are called random processes.
The implementation of the random function X (t) (sampling function) is a specific form that it takes as a result of experience. The implementation of a random process can be considered as an element of the set of possible physical realizations of a random process (Fig. 5.8). The set of realizations of a random process is called an ensemble of realizations. The set of realizations at a fixed point in time (a sample of random values) is called a cross section of a random process.

Fig. 5.8. Implementing a random process
In any section, a random process is a random variable.
The expectation of a random process is a function of time.
 (5.10)
(5.10)
The second central moment for two sections of a random process is called the covariance function
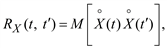 (5.11)
(5.11)
Where 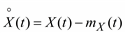 - centered random process.
- centered random process.
At t = t ′, the covariance function is equal to the variance of the random process.
 (5.12)
(5.12)
The mathematical expectation and the covariance function of a random process can be found by the realizations of the random process — by the averages by realizations:
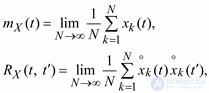 (5.13)
(5.13)
where N is the number of realizations of the random process.
If the expectation and covariance function are independent of time t, then the process is stationary:
 (5.14)
(5.14)
where τ = t ′ - t. In (5.14), the covariance function depends only on the magnitude of τ, and not on its location on the time axis (Fig. 5.9).
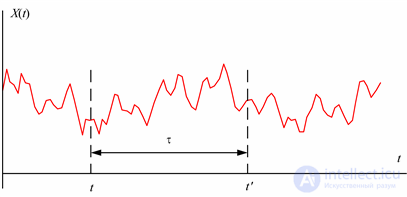
Fig. 5.9. The time between two sections of a random process
A possible view of the covariance function is shown in Fig. 5.10.
In many cases, the normalized covariance (or correlation) function is used. For stationary random process
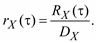 (5.15)
(5.15)
The magnitude of the correlation function | r X (τ) | ≤ 1.
The time averaging of individual sampling functions (implementations) is possible. For the k-th sampling function, we have:
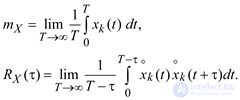 (5.16)
(5.16)
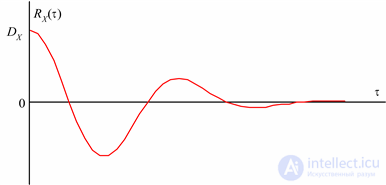
Fig.5.10. Covariance function of a random process
If the random process X (t) is stationary and the characteristics m X and R X (τ) are the same for different sampling functions, then this process is called ergodic.
Ergodic processes are an important class of random processes.
Non-stationary random processes are all random processes that do not have the properties of stationarity. These processes are complex in research, and often in analysis problems they are divided into stationarity intervals or approximated approximately by stationary processes.
Comments
To leave a comment
probabilistic processes
Terms: probabilistic processes