3.1 Pareto set. Classification of CRA under certainty

A common part of decision-making methods under many criteria is finding a set of Pareto-optimal alternatives from the entire set of alternatives. Consider the CRA under certainty - the set of outcomes coincides with the set of alternatives.

Let us use N criteria for evaluating outcomes, with a larger criterion value being preferable to a smaller one. Then each outcome (and alternative) will be characterized by a vector of criteria values ​​( x ₁ , x ₂ , ..., x _N ).

The vector ( x ₁ , x ₂ , ..., x _N ) contains full information about the value (utility) of this outcome for the decision maker, and the comparison of any two outcomes is replaced by a comparison of their vector estimates.

The vector estimate x = (x ₁ , x ₂ , ..., x _N ) dominates the Pareto vector estimate 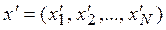(designation 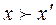) if for all 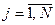inequality holds 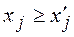and for at least one index j the inequality is strict.

Vector rating 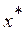is called Pareto optimal if there is no such vector estimate of x such that .

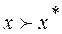Similarly for outcomes.

Alternative A ₁ dominates the alternative A ₂ , (designation 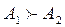) , if A _{1 is} not worse than A ₂ by all criteria , and at least one criterion is better, or if the vector estimate of outcome A ₁ dominates in Pareto vector estimation of outcome A ₂ .

An alternative is considered Pareto optimal if there are no alternatives dominating it.

The set of non-dominated alternatives forms the set of Edgeworth-Pareto (ER).

The task of identifying a set of EPs is usually considered as preliminary. It is followed by the most significant stage of decision making.

Different methods of decision-making with many criteria differ in the way of transition to a unified assessment of the utility of alternatives. There are a number of groups of such methods.

In the methods of the first group (direct methods), the dependence of the overall utility of an alternative on estimates by individual criteria is known in advance. The most commonly used type of dependence is that determines the numerical indicators of the importance of criteria (weights), multiplied by the estimates of the criteria (weighted sum method of evaluating the criteria).

In the second group of methods (compensation methods) they try to balance (compensate) the estimates by one alternative with the estimates of another, in order to find which estimates are better. In theory, this is the simplest method, in which a person writes out the advantages and disadvantages of each alternative and, eliminating pairwise equivalent advantages (disadvantages), studies what remains.

In the third group (methods of incomparability thresholds) the rule of comparison of two alternatives is set, in which one alternative is considered better than the other (for example, the first one is better by most criteria). In accordance with a given rule, alternatives are divided (in pairs) into comparable (one is better than the other, or equivalent) and incomparable. By measuring the relation of comparability, we get a different number of pairs of comparable alternatives.

In the fourth group (axiomatic methods) a number of properties are defined, which the dependence of the general utility of the alternative on the estimates by individual criteria must satisfy. These properties (called axioms) are verified by obtaining information from decision makers. In accordance with this information, a conclusion is made on one or another form of dependence.

3.2 Direct methods

For direct methods, the dependence of the utility of an alternative on its estimates by criteria is typical, which is set without any theoretical basis, and the parameters of this dependence are either also set or directly estimated by the decision maker.

3.2.1. Weighted amount method. The dependency is as follows:

,

where w _i is the weight (importance) of the i -th criterion assigned by the decision maker; x _i - evaluation of alternatives by i -th criterion.

The rationale for the weighted sum method is the idea of ​​the overall utility of the alternative as the sum of the estimates of several independent criteria. The coefficients w _i express the relative importance of the criteria estimates.

3.2.2. Multiplicative method. The dependency is as follows:

.

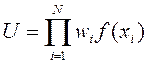Most often take f ( x _i ) = x _i . In some cases, using the method with the dependence f ( x _i ) = 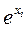. By logarithm, the multiplicative method can be reduced to the summation of logarithms of estimates, therefore, sometimes it is combined with the weighted sum method. The rationale for the multiplicative method is the idea of ​​evaluations by criteria as the probabilities of achieving certain quality indicators.

3.2.3. Lexicographic ordering. In this method, the criteria are sorted by importance, after which the alternative is considered to be the best, having a higher score by the more important criterion K ₁ , regardless of the other criteria. If the estimates for criterion K _{1 are the} same, the alternatives are compared by criterion K _2, and so on.

3.2.4. Bof method. This method is proposed in Bystrov Oleg Filaretovich for comparative evaluation of investment projects in a variety of indicators [7, p. 54-63].

The purpose of the method is to determine the most appropriate project for the given indicators.

This method can be used to evaluate any set of objects for a variety of indicators (criteria) - decision-making with many criteria under certainty.

Formulation of the problem

Given:

K is the number of objects, M is the number of indicators for comparing objects;

R = ( R ₁ , R ₂ , ... R _M ) - ranking of indicators by importance;

| C _ij | - matrix of values ​​of indicators for objects .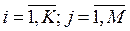

You want to arrange the objects or choose the best object.

Algorithm Description

The BOP method consists of the following steps .

1. Select the optimal number of indicators. Denote indicators .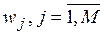

2. Rank the indicators by importance in accordance with the preferences of the decision maker. Denote the ranks of indicators .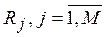

3. To determine the weights of each indicator.

Weight coefficients w _j determined by the formula 3.2.1 and then normalized by the formula 3.2.2:

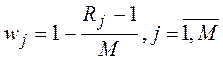	(3.2.1)
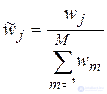	(3.2.2)

4. Rank the objects in importance in accordance with the preferences of the decision maker for each indicator. Denote the values ​​of the indicators for the objects P _ji , the ranks of the objects by indicators 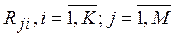where K is the number of objects.

5. Determine the weighting factors of each object for each indicator.

The weights of the objects for each indicator 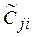are determined by the formula 3.2.3 and then normalized by the formula 3.2.4:

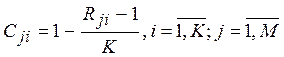	(3.2.3)
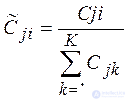	(3.2.4)

Thus, for calculating weights, order relations between objects are used. However, the use of order information may lead to the loss of some useful information. If it is necessary to take into account quantitative information, weighting factors of indicators are calculated using the formula 3.2.5, if larger values ​​of indicators are preferable to smaller ones, or according to formula 3.2.6, if smaller values ​​are preferable to larger ones. In this stage 4 (ranking of objects for each indicator) is omitted.

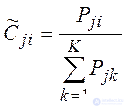(3.2.5)

P _ji - the value of the indicator j for the object i .

(3.2.6)

6. To calculate the values ​​of the generalized indicator for each object.

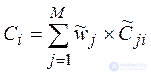(3.2.7)

7. Rank the objects in accordance with the values ​​of generalized indicators and / or determine the best object.

Example

It is required to choose the best investment project for implementation. For comparison of projects, the following indicators were selected:

NVP (net present value);

IRR (internal rate of return);

PI (profitability index);

PP (payback period);

ARR (cf. rate of return on investment).

Information about the projects is presented in Table. 3.1, ranking indicators by importance - in Table. 3.2.

Table 3.1

Project Information

Table 3.2

Ranks of indicators

Thus, stage 1 and stage 2 have already been completed.

Stage 3. Determination of weighting factors of indicators and rationing of their values.

, , , , .

, , , , .

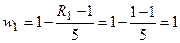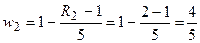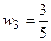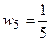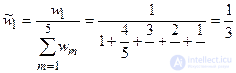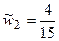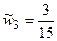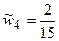Stage 4. Ranking of objects for each indicator.

Projects are compared for each indicator and the results are recorded in table 3.3, R _ji is the rank of the object with number i by indicator with number j .

Table 3.3

Project Rank by Indicator

Step 5. Determination of the weighting coefficients of the objects for each indicator and rationing the obtained values.

Calculate the values ​​of the indicator 1 for all objects.

, ,

, .

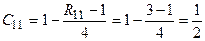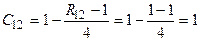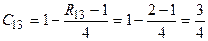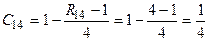We normalize the values ​​obtained.

, ,

, .

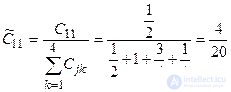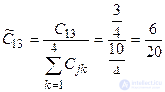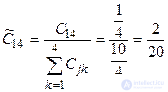The values ​​of the remaining weighting coefficients of objects on indicators are calculated similarly.

Stage 6 . The calculation of the values ​​of the generalized indicator for objects.

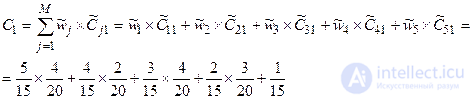
Similarly, we calculate , , .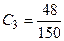

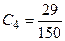Stage 7. Thus, project 3 is the best, project 2 comes second, followed by projects 4 and 1.