Knowledge representation

The concept of a formal system

The appearance of formal systems was due to the realization that completely different systems, be they technical, social, economic, or biological, have a deep resemblance. In the formal system (FS), operating with various symbols, these symbols are perceived simply as elements that are treated according to certain rules, depending only on the form of expressions formed from symbols. The concept of truth appears only in connection with possible applications (interpretations) of this system. Formal systems are axiomatic systems, i.e. systems with the presence of a certain number of original pre-selected and fixed statements, called axioms. A formal system is considered given if the following conditions are met.

• Given a set consisting of a finite or infinite number of elements, which are called terms. There is another finite set whose elements are bundles or operations.
• Any linear ordered set of terms and operations is called a formula. From the set of formulas allocate subsets of properly constructed formulas (PPF). For the PPF, the rules for their construction are specified, i.e. an effective procedure is determined, which allows to find out by this expression whether it is a FPP in a given FS.
• Selected some set of PPF, called FS axioms. In this case, there must be an effective procedure that allows for an arbitrary FPD to decide whether it is an axiom.
• There is a finite set of relations R1, R2, ..., Rk between FPPs called inference rules. The concept of "output" should also be effective, i.e. there must be an effective procedure that allows for an arbitrary finite sequence of the FFT to decide whether each member of this sequence can be derived from one or more of the preceding FPS using some fixed inference rules. The FS derivation is any PPS A1, A2, ..., An sequence such that for any i (i =) FFT Ai is either the FS axiom, or a direct consequence of any previous FFT according to one of the derivation rules.

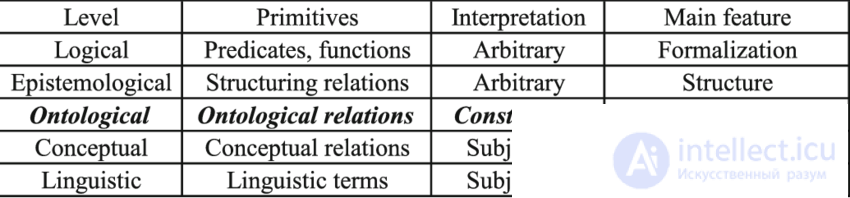
PPF B is called a FS theorem if there is a FS output in which the last PDF is B. Any FS is given by a quadruple where T is the set of terms and operations; H - a set of rules for designing PPF; A is a system of axioms; R is a set of inference rules. It is possible to extend the formal system by introducing additional rules to the sets H, A and R. If the set H is affected by the rules h changing the syntax of the FS, the set A is the rules changing the axiom system, and if the FS allows you to change the set of output rules using some , then such an extension of the FS is called a semiotic system.

For the functioning of a semiotic system, it is necessary to set a problem-oriented formal system and the rules for its change. The formal system itself is neither a language nor a system of knowledge, it does not contain any statements about objects, but is simply a calculus - some kind of actions according to certain rules over sequences of terms. Two classes of formal systems are the mathematical basis for constructing AI systems: propositional calculus and first-order predicate calculus.

Calculus of statements as a formal system

A complex statement has a truth value that is uniquely determined by the truth values ​​of the simple statements from which it is composed.

For example: "If a student goes to bed late and drinks coffee, in the morning he will get up in a bad mood or with a headache." This complex sentence consists of the following simple sentences:

• "Student go to bed late"
• "A student drinks coffee at night"
• "In the morning the student will get up in a bad mood"
• "In the morning the student will get up with a headache."

Denoting a complex sentence by X, and simple ones, respectively, by Y, Z, U, V, we can write

X = if Y and Z, then U or V

Or X = (Y and Z) → (U or V)

Each logical connective can be viewed as an operation that forms a new utterance — a complex of simpler ones. Thus, any complex statement can be written in the form of a formula containing logical connectives and symbols that denote simple sentences, called atoms. To find out whether a statement is true or false, it is enough to know the true meaning of all the atoms from which it is composed.

Let the formula B and X1, X2, ..., Xn be given are the atoms found in it. Then by the interpretation of the formula B we mean the attribution of true values ​​to the atoms X1, X2, ..., Xn. The formula B is true in this interpretation if and only if B assumes the value "true", otherwise B is false in this interpretation. For a formula consisting of n atoms, there are 2n interpretations.

The formula for calculating propositions, which is true in all interpretations, is called a tautology or a generally valid formula. Examples of tautologies are X or not (X), X → (Y → X). The formula for calculating statements is called a contradiction if it is false in all interpretations. For example, X and not (X). Let us consider without proof several rules for the formation of tautologies from tautologies (it is obvious that in order to obtain contradictions it is necessary to apply the operation of denial to tautology).

Let B be some formula, and B * be a formula obtained from B by substituting formula C instead of atom X wherever it occurs in B. Then, if B is a tautology, then B * is also a tautology. This rule is called in the FS substitution rule. If B and B → C are tautologies, then C is also tautology. This result is known as the rule of deductive inference - modus ponens.

The theory of deductive inference (a section of mathematical logic) deals with the derivation of statements from the initial list of reasoning, facts, assumptions, axioms. By giving interpretations in which the premises are true, a true conclusion is also obtained.