Lecture
In complex analysis, the deduction of a given object (function, form) is an object (number, form, or cohomological class of a form) that characterizes the local properties of a given one.
The theory of residues of a complex variable was mainly developed by O. Cauchy in 1825–1829. Besides him, important and interesting results were obtained by S. Hermite, J. Sohotsky, E. Lindelöf and many others.
In 1887, A. Poincaré generalized the Cauchy integral theorem and the notion of residue to the case of two variables [1] , from this moment the multidimensional theory of residues originates. However, it turned out that this concept can be generalized in various ways.
To denote the analytical function deduction 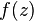 at the point
at the point 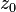 expression is applied
expression is applied  from English Residue . In some literature it is designated as
from English Residue . In some literature it is designated as 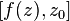 [2] .
[2] .
Let be 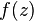 - complex-valued function in the region
- complex-valued function in the region 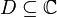 holomorphic in some punctured neighborhood of a point
holomorphic in some punctured neighborhood of a point 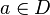 .
.
Deduction function 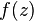 at the point
at the point 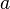 called number
called number
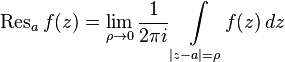 .
. Since the function is holomorphic 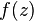 in a small punctured neighborhood of a point
in a small punctured neighborhood of a point 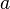 according to the Cauchy theorem, the value of the integral does not depend on
according to the Cauchy theorem, the value of the integral does not depend on 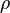 for sufficiently small values of this parameter, as well as on the form of the path of integration. It is only important that the path is a closed curve in the domain of the analyticity of the function, which once covers the point in question and no other points belonging to the domain of holomorphy.
for sufficiently small values of this parameter, as well as on the form of the path of integration. It is only important that the path is a closed curve in the domain of the analyticity of the function, which once covers the point in question and no other points belonging to the domain of holomorphy. 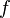 .
.
In some neighborhood of a point 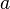 function
function 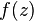 seems to converge near laurent by degrees
seems to converge near laurent by degrees 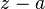 . It is easy to show that the deduction coincides with the coefficient of the series
. It is easy to show that the deduction coincides with the coefficient of the series 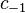 at
at 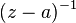 . Often this representation is taken as the definition of the function deduction.
. Often this representation is taken as the definition of the function deduction.
To enable a more complete study of the properties of a function, the concept of residue at infinity is introduced, and it is considered as a function on the Riemann sphere. Let the infinitely remote point be an isolated singular point. 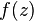 , then a deduction at infinity is called a complex number, equal to
, then a deduction at infinity is called a complex number, equal to
 .
. The integration cycle in this definition is oriented positively, that is, counterclockwise.
Similar to the previous case, the residue at infinity has a representation in the form of the coefficient of the Laurent decomposition in the neighborhood of the infinitely distant point :
 .
. From the point of view of analysis on manifolds, to introduce a special definition for some selected point of the Riemann sphere (in this case, infinitely remote) is unnatural. Moreover, such an approach is difficult to generalize to higher dimensions. Therefore, the concept of deduction is introduced not for functions, but for differential 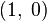 -forms on the Riemann sphere:
-forms on the Riemann sphere:
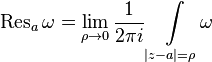 .
. At first glance, there is no difference in definitions, but now 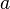 - arbitrary point
- arbitrary point 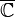 , and the change of sign in the calculation of the deduction at infinity is achieved by changing the variables in the integral.
, and the change of sign in the calculation of the deduction at infinity is achieved by changing the variables in the integral.
Integral 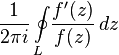 called the logarithmic function residue
called the logarithmic function residue 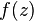 relative to the contour
relative to the contour 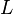 .
.
The notion of a logarithmic residue is used to prove the theorem of Rushe and the main theorem of algebra
According to the definition, a deduction can be calculated as a contour integral, but in the general case it is rather laborious. Therefore, in practice, they mainly use the consequences of the definition:
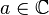 , as well as at the point of regularity, the deduction of the function
, as well as at the point of regularity, the deduction of the function 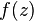 equals zero. At the same time, this statement is not true for an infinitely remote point. For example, the function
equals zero. At the same time, this statement is not true for an infinitely remote point. For example, the function 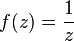 has a first-order zero at infinity, however
has a first-order zero at infinity, however 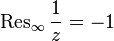 . The reason for this is that the form
. The reason for this is that the form 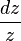 has a peculiarity both at zero and at infinity.
has a peculiarity both at zero and at infinity. 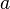 multiplicities
multiplicities 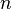 deduction can be calculated by the formula:
deduction can be calculated by the formula:  ,
, special case 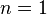
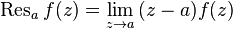 .
.  has a simple pole at a point
has a simple pole at a point 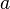 where
where  and
and 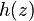 holomorphic in the neighborhood
holomorphic in the neighborhood 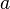 functions,
functions, 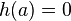 ,
, 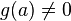 , then you can use a simpler formula:
, then you can use a simpler formula: 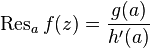 .
. 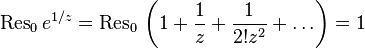 , as the coefficient at
, as the coefficient at  equals 1.
equals 1. In most cases, the theory of residues is used to calculate various kinds of integral expressions using the main theorem on residues. Often useful in these cases is the Lemma of Jordan.
Let function 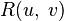 - rational function of variables
- rational function of variables 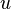 and
and 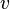 . To calculate the integrals of the form
. To calculate the integrals of the form 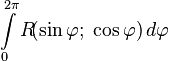 It is convenient to use Euler formulas. Putting that
It is convenient to use Euler formulas. Putting that 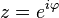 , and making the appropriate transformations, we get:
, and making the appropriate transformations, we get:
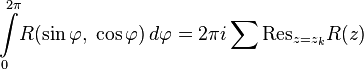 .
. To calculate improper integrals using the theory of residues use the following two lemmas:
1. Let the function 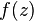 holomorphic in the upper half-plane
holomorphic in the upper half-plane 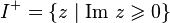 and on the real axis except for a finite number
and on the real axis except for a finite number 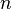 poles not lying on the real axis and
poles not lying on the real axis and 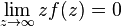 . Then
. Then
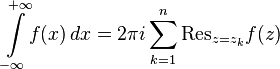 .
. 2. Let the function 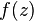 holomorphic in the upper half-plane
holomorphic in the upper half-plane 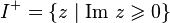 and on the real axis except for a finite number
and on the real axis except for a finite number 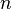 poles not lying on the real axis
poles not lying on the real axis 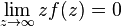 and
and 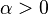 . Then
. Then
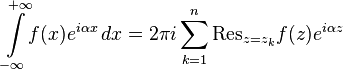
Moreover, the integrals in the left-hand sides of equalities are not obliged to exist and, therefore, are understood only in the sense of the principal value (Cauchy formula).
 | This section is not complete. You will help the project by correcting and adding it. |
 | This section is not complete. You will help the project by correcting and adding it. |
 | This section is not complete. You will help the project by correcting and adding it. |
Comments
To leave a comment
Comprehensive analysis and operational calculus
Terms: Comprehensive analysis and operational calculus