Lecture
Biquaternions - complexification (expansion) of ordinary (real) quaternions.
Biquaternions can be described as sets of numbers of the form “ 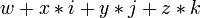 ", Where w, x, y, z - there are certain" special complex numbers. " Alternative method of introduction - Cayley-Dixon procedure: these are hypercomplex numbers of the form “
", Where w, x, y, z - there are certain" special complex numbers. " Alternative method of introduction - Cayley-Dixon procedure: these are hypercomplex numbers of the form “ 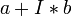 ", Where a, b - any quaternions, and I -" imaginary unit of expansion ". Three different types of biquaternions are known, depending on what type of “complex” numbers are the basis of this representation (in other words, what are the properties of an expandable multiplication operation for the number “ I ”):
", Where a, b - any quaternions, and I -" imaginary unit of expansion ". Three different types of biquaternions are known, depending on what type of “complex” numbers are the basis of this representation (in other words, what are the properties of an expandable multiplication operation for the number “ I ”):
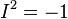 );
); 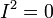 );
); 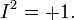 )
) Hamilton wrote about ordinary biquaternions in 1844. (see Proceedings of the Irish Royal Academy 1844 and 1850 p. 388). Among the most prominent supporters of these biquaternions should be Alexander Macfarlane (en: Alexander Macfarlane), Arthur U. Conway, Ludwik Silberstein (en: Ludwik Silberstein) and Cornellius Lanczos. The unit quasi-sphere of biquaternions provides a representation of the Lorentz group, on which the special theory of relativity is based.
Double Quaternions studied by Clifford, William. Dual quaternions instrumentally provide nonstandard analysis of ordinary quaternions. Further, if not specified, we are talking about ordinary biquaternions.
“The algebra of biquaternions” is a tensor product of algebras C ⊗ H (taken over real numbers), where C is one or another algebra of complex numbers, and H is an algebra of ordinary (real) quaternions. As a C- algebra, biquaternions are isomorphic to the algebra of complex matrices 2x2 M 2 ( C ).
...
There are three complex matrices for which: 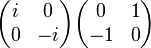 =
= 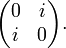 Moreover, the square of each of these matrices is “minus the identity matrix”, and if the product of these matrices is the product of the numbers i * j = k; j * i = -k . We obtain that the subgroup of the matrix group generated by these matrices is isomorphic to the quaternion group. Therefore, if we compare the matrix
Moreover, the square of each of these matrices is “minus the identity matrix”, and if the product of these matrices is the product of the numbers i * j = k; j * i = -k . We obtain that the subgroup of the matrix group generated by these matrices is isomorphic to the quaternion group. Therefore, if we compare the matrix 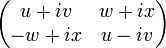 biquaternion q == u * 1 + v * i + w * j + x * k , then for a given 2 × 2 complex matrix, there are always complex quantities u, v, w, x in this form. In other words, the ring of complex matrices is isomorphic to [1] the ring of (ordinary) biquaternions.
biquaternion q == u * 1 + v * i + w * j + x * k , then for a given 2 × 2 complex matrix, there are always complex quantities u, v, w, x in this form. In other words, the ring of complex matrices is isomorphic to [1] the ring of (ordinary) biquaternions.
When considering (ordinary) biquaternions as an algebra over the field of real numbers R , the set {1, I, i, Ii, j, Ij, k, Ik} forms a basis, this algebra has a real dimension of space eight. Moreover, the squares of all the elements Ii, Ij, Ik = "+ 1". Hence, the real subalgebra formed 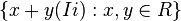 is isomorphic to a ring that is formed by double numbers (with an algebraic structure similar to being built over a single hyperbola). The elements Ij, Ik define the same subalgebra.
is isomorphic to a ring that is formed by double numbers (with an algebraic structure similar to being built over a single hyperbola). The elements Ij, Ik define the same subalgebra.
Items 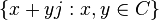 form a subalgebra isomorphic to bicomplex numbers (tessarine).
form a subalgebra isomorphic to bicomplex numbers (tessarine).
The third type of subalgebra, the so-called. “Cockaternions”, generated by Ij, Ik , because a real linear subspace with a basis {1, i, Ij, Ik} is closed by multiplication (because Ij * Ik = -i). This basis forms the dihedral group of a square, and Cockavernions are isomorphic to the algebra of real 2x2 matrices.
Quantum mechanics and spinor algebra interpret the biquaternions Ii, Ij, Ik (or their negation), regarding them in the presentation M (2, C), as Pauli matrices.
Comments
To leave a comment
Algebra
Terms: Algebra