Lecture
When the surface is deployed on a plane, each point of the surface corresponds to a single point on the scan: the surface line passes into the scan line; lengths of lines, values of flat angles and areas bounded by closed lines remain unmeasured. Thus, the process of building a sweep is reduced to finding the natural (true) value of each surface element and displaying them on a plane.

Fig. 146

Fig. 147
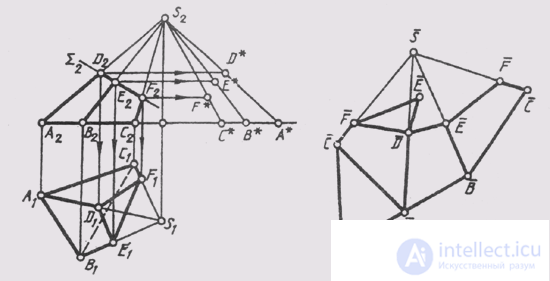
Fig. 148

Fig. 149
Each side face on the scan is constructed as a triangle on three sides. CS is the shortest lateral edge, therefore it is more rational to mentally cut a pyramid along this edge.
To plot the points D, E and F corresponding to the vertices of the pyramid section by the Sum plane, you need to determine the true distances of these points from the top S. After constructing the side face sweep of the truncated part of the pyramid, you need to attach the ABC and DEF triangles to it. and the cross section of the pyramid.
In fig. 149 the method of triangulation is used to develop a scan of the conical surface, which is replaced by the surface of the twelve-sided pyramid inscribed into it. The sweep is a symmetrical figure, since the surface has a plane of symmetry Sum. In this plane lies the shortest generatrix of S-6. On it and made a cut surface. The longest generator S-0 is the axis of symmetry of the surface sweep.
The natural values of the generators are determined with the help of right triangles, as in the previous problem in fig. 149. From the axis of symmetry S - 0, we build six in one direction and six in the other direction of adjacent triangles with a common vertex S. Each of the triangles is built on three sides, with two
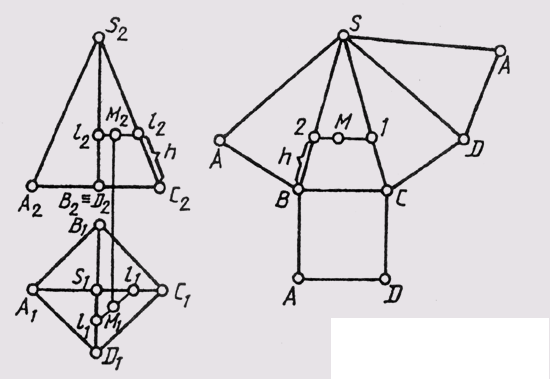
Fig. 150
The pons are equal to the true values of the generators, and the third to the chord, which tightens the arc of the base circumference between adjacent division points. The sweep points O, 1, 2, ... are connected. The construction of a sweep is greatly simplified if the surface is represented by a straight pyramid of regular shape or a right circular cone. In fig. 150 shows a scan of a tetrahedral straight pyramid. Its construction is simplified by the fact that the generators of the AS and CS pyramids are parallel to the frontal plane of the projections and projected onto it in full size. The base of the ABCD pyramid lies in a plane parallel to the horizontal plane of the projections, and is projected on it in full size. To build a sweep, it is enough to build an AS side and make the notches with an arc radius equal to BS and AB from points S and A, respectively, we get point B , etc. But the full-size base can be built on the basis of one of its sides (in Fig. 150 - on the basis of the AB side ). The position of the point on the surface of the pyramid sweep is determined in the following order: through the frontal projection of the point M (M 2 ), we draw a horizontal line to the intersection with the edges A 2 S 2 and B 2 S 2 . We will get points 11 and 22. On line AS of the sweep from point A we put off segment h and from the obtained point 1 we will draw line 1, 2 parallel to AD on which we will put point M in the position it occupies on the horizontal projection of line 1, 2.
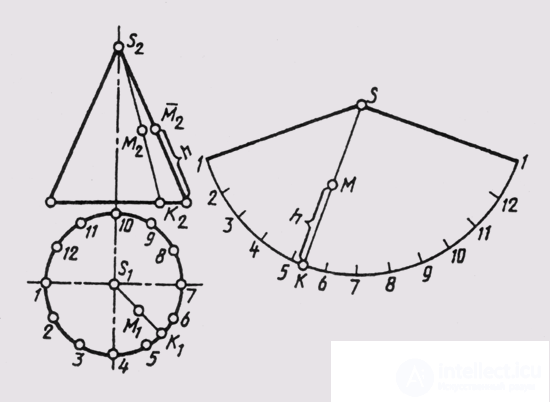
Fig. 151
In fig. 151 shows an example of constructing a sweep of a right circular cone. To build it, we use the fact that the essay generator of the cone l on the frontal plane was depicted in full size. Choosing the position of the sweep apex - a point S, with a radius L, we draw an arc and lay 12 equal parts on it, into which the circumference of the base of the cone, shown on the horizontal projection plane in full size, was divided. The more we divide a circle into more equal sections, the more accurately we will construct a sweep. The position of the point M on the scan of the surface of the cone is determined as follows: through the frontal projection of the point, we draw the generator and construct its horizontal projection. We find that the generator has crossed the base of the cone between points 5 and 6. We transfer the point K to the sweep arc, placing it between points 5 and 6, and connect it to the vertex of the cone sweep S. From the point M 2 we draw a horizontal line to the intersection with the essay generator L and get the point M 2 . The distance from the base of the cone to the point M 2 along the generatrix is the height of the point that we lay on the scan from the point K on the KS line . The resulting point will determine the true position of point M on the scan. Thus, we construct the scan of a conical surface using neighboring points of the base circle, into which a regular pentagon is inscribed, i.e., the conical surface is conventionally replaced by a surface inscribed with a regular pentagonal pyramid, and the triangulation method is used to construct the scan.
Comments
To leave a comment
11. Metric tasks
Terms: 11. Metric tasks