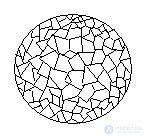
We describe a convex polyhedron with small faces near the sphere. Let S` be the surface area of a polyhedron, i.e. the sum of the areas of its faces. Let us find the approximate value of the surface area of the polyhedron, assuming that the linear dimensions of the faces, i.e. the distance between any two points of any face, less than ε.
The volume of the polyhedron is equal to the sum of the volumes of the pyramids, having their bases the faces of the polyhedron, and the vertex is the center of the sphere. Since all pyramids have the same height, equal to the radius R of the sphere, the volume of the polyhedron
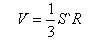
The volume of the polyhedron is larger than the volume of the sphere bounded by the sphere, but smaller than the volume of the sphere with the same center and with radius R + ε. In this way,
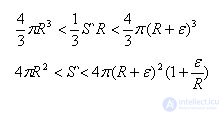
The surface area of the described polyhedron with an unlimited reduction in the size of its faces, i.e. with an unlimited decrease in ε, tends to 4πR ^ 2 and therefore this quantity is taken as the area of the sphere.
The area of the sphere of radius R is calculated by the formula
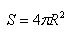
The area of the spherical part of the surface of the spherical sector is determined similarly, i.e. the area of the spherical segment, for it is obtained the formula
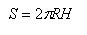
where H is the height of the segment.

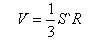
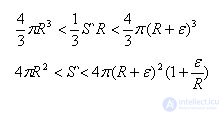
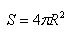
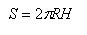
Comments
To leave a comment
Stereometry
Terms: Stereometry