Lecture
This section discusses standard inference patterns that can be used to form a chain of conclusions leading to a desired goal. These inference templates are called inference rules . The most widely known rule is called the branch rule (Modus Ponens - modus ponens) and is written as follows:
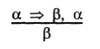
This record means that if any statements are given in the form α => β and a, then the statement β can be derived from them. For example, if given (WumpusAhead ^ WumpusAlive) => Shoot and (WumpusAhead l WumpusAlive), then we can derive the statement Shoot.
Another useful rule of inference is the rule of removing the "AND" bundle , which states that any of its conjuncts can be derived from a conjunction:
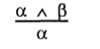
For example, from the statement (WumpusAhead ^ WumpusAlive) we can derive the statement WumpusAlive. Considering the possible truth values of α and β, one can easily show that the rule of separation and the rule of removing the ligament "AND" are consistent not only in relation to these examples, but also to all possible statements. This means that these rules can be used in all specific cases in which they may be required, producing consistent logical conclusions without having to go through all the models.
As logical inference rules, you can also apply all logical equivalences shown in the listing. For example, from the equivalence of a two-sided implication and two implications, the following two rules of inference can be obtained (the first of them is called the rule of removing a two-sided implication ):
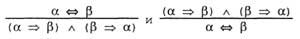
But not all inference rules work in both directions, like this. For example, you cannot apply the separation rule in the opposite direction to get the statements α => β and a from the statement β.
Consider how you can use these rules of inference and equivalence in the world of vampus. We start with the knowledge base containing the statements R 1 —R 5 , and show how to prove the statement ¬P 1,2 , i.e. the assertion that there is no hole in the square [1,2]. We first apply the rule of removing a two-sided implication to the statement R 2 in order to obtain the following:
R 6 : (B 1,1 => (P 1,2 v P 2,1 )) ^ ((P 1,2 v P 2,1 ) => B 1,1 )
Then apply to the statement R 6 the rule of removing the bunch "AND" and get:
R7: ((P 1,2 v P 2,1 ) => B 1,1 )
From the logical equivalence of negations follows:
R 8 : (¬B 1,1 => ¬ (P 1,2 v P 2,1 ))
You can now apply the separation rule to R 8 and R 4 with perception data (i.e. ¬B 1,1 ) to get the following:
R9: ¬ (P 1,2 v P 2,1 )
Finally, we apply the de Morgan rule, which allows us to get this conclusion:
R10: ¬P 1.2 ^ ¬P 2.1
This means that neither squared [1,2] nor squared [2,1] has a hole.
The above process of inference (the sequence of application of the rules of inference) is called proof. The process of forming evidence is completely analogous to the process of finding solutions in search problems. In fact, if it were possible to formulate the function of determining a successor to develop all possible options for applying the rules of logical inference, this would allow using search algorithms to form evidence. Thus, instead of laboriously iterating over models, a more effective method of logical inference can be used - the formation of evidence. The search can go in the forward direction, from the initial knowledge base, and is carried out by using inference rules to get the target statement, or the search can be done in the opposite direction, from the target expression, in an attempt to find a chain of inference rules leading from the original base. knowledge. Below in this section, two families of algorithms are considered that use both of these approaches.
From the fact that the problem of logical inference in propositional logic is NP-complete, it follows that in the worst case, the search for evidence may not be more effective than the search for models. However, in many practical cases, the search for evidence can be extremely effective simply because it can ignore irrelevant (irrelevant) statements, no matter how large their number.
For example, in the above proof, leading to the statement ¬P 1,2 ^ ¬P 2.1 , the statements B 2.1 , P 1.1 , P 2.2, or P 3.1 were not mentioned. They could not be considered, since the target statement, P 1,2 , is present only in the statement R 4 ; the other statements from the composition of R 4 are present only in R 4 and R 2 , therefore R 1 , R 3 and R 5 have no relation to the proof. The same reasoning will remain fair if a million more statements are entered into the knowledge base; on the other hand, in this case, a simple algorithm for searching the rows in the truth table would be literally suppressed due to the exponential explosion caused by the rapid increase in the number of models.
This property of logical systems actually follows from a much more fundamental property, called monotonicity . According to this property, the set of statements that can be obtained by logical inference increases only as new information is added to the knowledge base. For any statements α and β, the following is true:
if KB ≠ α, then KB ^ β ≠ α
For example, suppose the knowledge base contains an additional statement β, according to which there are exactly eight holes in this instance of the vampus world. This knowledge may help the agent to come to additional conclusions, but they are not able to call into question any conclusion already made by α, in particular the conclusion that there is no hole in the square [1,2]. Monotonicity means that the rules of logical inference can be applied every time the appropriate prerequisites are found in the knowledge base — the resulting conclusion will be a consequence of this rule, regardless of what else is in the knowledge base.
Comments
To leave a comment
Knowledge Representation Models
Terms: Knowledge Representation Models