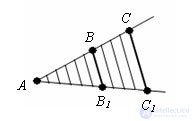
Theorem. Parallel straight lines intersecting the angle cut off proportional segments from the angle sides.
 Evidence.
Evidence. Let the sides of angle A intersect parallel lines at points B, B
1 , C, C
1 . The theorem states that
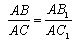
Divide the segment AC into n equal parts. Let δ be the length of the division segment and AC = nδ.
Two cases are possible:
1) There is n such that B is a division point. That is, there is m <n such that AB = mδ. We draw through the dividing points of the segment AC straight lines parallel to the straight line CC
1 . By the Thales theorem, these straight lines divide the segment AC1 into equal segments of some length δ
1 . We get AB
1 = mδ
1 , AC
1 = nδ
1 . From this
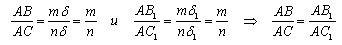
2) For no n, B
1 is not a division point. Assume that
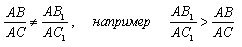
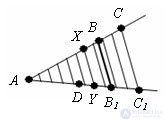
Let us put on line AC
1 segment AD = (AC
1 / AC) * AB. Moreover, AD <AB
1 . We divide AC
1 into a sufficiently large number n equal parts. We draw through the dividing points straight lines parallel to SS
1 . If n is sufficiently large, on the segment DB
1 there will be division points. Denote one of them as a point Y and draw through it a straight parallel SS
1 that intersects the ray AC at the point X. By the proven
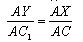
Replace AY with a smaller value AD, and AX with a larger value AB. Then
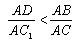
From here
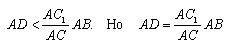
That contradicts the construction of the segment AD. The theorem is proved.

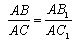
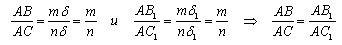
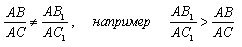

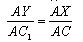
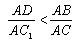
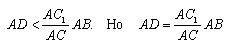
Comments
To leave a comment
Planometry
Terms: Planometry