Lecture
Prim's algorithm takes a square matrix (representing a graph with weighted arcs) and finds the arcs that form the minimum skeleton. ...
You can re-enter the values (you may need to manually change the symmetric values) and recalculate the solution. The program does not work if the minimum spanning tree is over one billion in weight. This implementation always starts from line 1. The arcs used are highlighted in red.
If the graph is not connected a spanning tree will be found (but some arcs can be selected).
If the graph is connected, the arcs used will be highlighted and the total weight will be calculated.
Now enter the weights of the arcs. Symmetrical values are entered automatically. Leave blank cells for which there are no arcs.
| node 1 | node 2 | node 3 | node 4 | node 5 | |
| node 1 | |||||
| node 2 | |||||
| node 3 | |||||
| node 4 | |||||
| node 5 |
Launch Prim!
1. enter the dimension of the matrix
2. fill in the incidence matrix for your graph
3. click "run Prim"
4. select the desired arcs on your graph included in the main tree, check the total weight
example of calculating and converting a graph into a matrix in the picture below
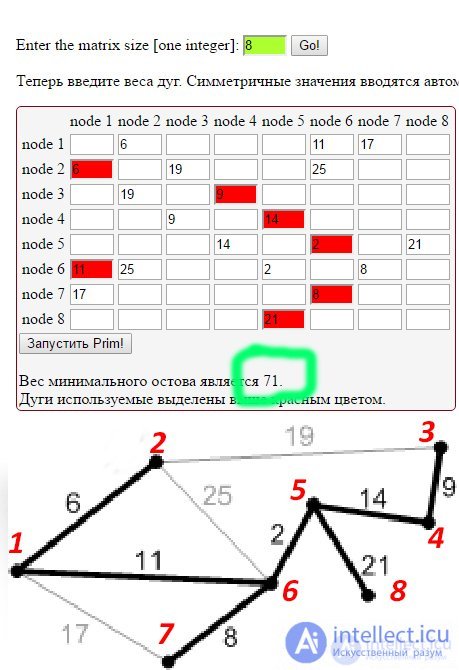
The problem of constructing a minimum spanning tree occurs in various fields. An interesting application of it is the problem of constructing a mixed spanning tree ( Dana Richards and Jeffrey S. Salowe. Mixed spanning trees in theory and practice. International Journal of Computational Geometry & Applications. Vol. 9, No. 3 (1999), 277-292 ): construct a tree for the graph with the properties of a minimal spanning tree and a tree of shortest paths. Another important task is to quickly update the minimum spanning tree when the graph changes. The article Sajal K. Das, Paolo Ferragina "An Erew Pram algorithm for updating minimum spanning trees" shows how to graph with n vertices and edges m update one edge of an accounting time O (logn).
The problem of constructing a minimum spanning tree is quite versatile, and continues to be investigated today. This article presents only basic algorithms. You can familiarize yourself with more advanced algorithms by reading the articles from the list of used literature.
Kruskal's algorithm combines the vertices of a graph into several connected components, each of which is a tree. At each step, from all the edges connecting vertices from different connected components, the edge with the least weight is selected. You need to check that it is safe. The safety of an edge is guaranteed by the previously proved theorem on safe edges. Since the edge is the lightest of all the edges exiting this component, it will be safe.
It remains to understand how to implement the choice of a safe edge at each step. For this, in Kruskal's algorithm, all edges of the graph G are enumerated in increasing weight. For the next edge, it is checked whether the ends of the edge lie in different connected components, and if so, the edge is added and the components are combined.
It is convenient to use for storing components of a data structure for disjoint sets, such as lists or, better, a forest of disjoint sets with path compression and rank join (one of the fastest known methods). The elements of the sets are the vertices of the graph, each set contains the vertices of one connected component. The following procedures are used to work with sets:
| Make-Set (v) | Creating a set from a set of vertices |
| Find-Set (v) | Returns the set containing the given vertex |
| Union (u, v) | Combines sets containing vertex data |
The general scheme of the algorithm looks like this:
MST-KRUSKAL (G, w)
1: A ← 0
2: foreach (for each) vertex v ∈ V [G]
3: do Make-Set (v)
4: order edges by weight
5: for (u, v) ∈ E (in increasing order of weight)
6: do if Find-Set (u) ≠ Find-Set (v) then
7: A ← A ∪ {(u, v)}
8: Union (u, v)
9: return A
Figures K1-K8 show the operation of the algorithm.
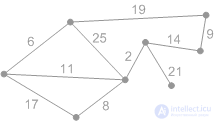 Figure: K1. Initial phase. The minimum covering forest is empty. |
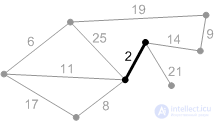 Figure: K2. We iterate over the edges in increasing order of weight: the first edge with weight 2. Add it to A. |
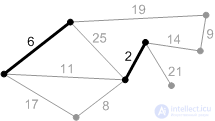 Figure: K3. The next safe edge with weight 6. Add it. |
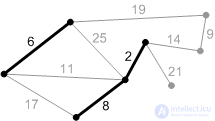 Figure: K4. |
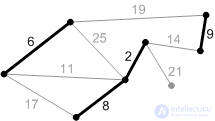 Figure: K5. |
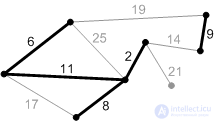 Figure: K6. |
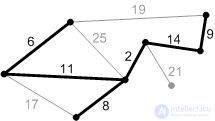 Figure: K7. |
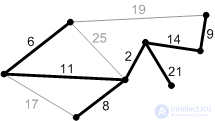 Figure: K8. Ribs weighing 17, 19 and 25 are not safe. Their ends lie in the same connected component. An edge with a weight of 21 is safe, so we add it. The minimum spanning tree has been constructed. |
Let's calculate the running time of the algorithm. We will assume that the method with union by rank and compression of paths ( [1] , 21.3) is used to store disjoint sets , since this is the fastest method known today. The initialization takes O (V) time, the ordering of the edges on line 4 is O (ElogE). Further, O (E) operations are performed, which together take time O (Eα '(E, V)), where α' is the function inverse to the Ackermann function (see [1], 21.4). Since α '(E, V) = o (logE), the total running time of Kruskal's algorithm is O (ElogE) (most of the time is spent on sorting).
Like Kruskal's algorithm, Prim's algorithm follows the general scheme of the algorithm for constructing a minimum spanning tree: at each step, we add a safe edge to the spanning tree under construction. Prim's algorithm belongs to the group of algorithms for growing the minimum skeleton: at each step, there is at most one non-trivial (not consisting of one vertex) connected component, and each edge of the least weight is added to it, connecting the vertices of the component with the other vertices. By the theorem, such an edge is safe.
When implementing, you need to be able to quickly select a safe edge at each step. It is convenient to use a priority queue (heap) for this. The algorithm receives as input the graph G and its root r - the vertex on which the minimum skeleton will grow. All vertices of G that have not yet entered the tree are stored in a queue with priority Ω. The priority of the vertex v is determined by the value of key [v], which is equal to the minimum weight of the edges connecting v with the vertices of the minimum skeleton. The p [v] field for tree vertices points to the parent, and for queued vertices, points to the tree node to which the edge with weight key [v] leads (one of these edges, if there are several).
Then Prim's algorithm looks like this:
MST-PRIM (G, w, r)
1: Ω ← V [G]
2: foreach (for each) vertex u ∈ Ω
3: do key [u] ← ∞
4: key [r] ← 0
5: p [ r] = NIL
6: while (for now) Ω ≠ 0
7: do u ← EXTRACT-MIN (Ω)
8: foreach (for each) vertex v ∈ Adj (u)
9: do if v ∈ Ω and w (u, v) then
10: p [v] ← u
11: key [v] ← w (u, v)
Figures A1-A8 show a diagram of the operation of Prim's algorithm with a root r.
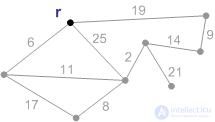 Figure: P1. Initial phase. The minimum covering forest consists of a root and an empty set of edges. |
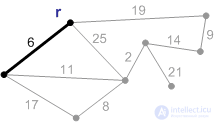 Figure: P2. An edge with weight 6 is the minimum edge connecting the root to the rest of the vertices. Add it to the minimum skeleton. |
 Figure: P3. The next safe edge with weight 11. Add it. |
 Figure: P4. |
 Figure: P5. |
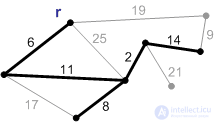 Figure: P6. |
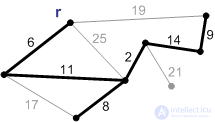 Figure: P7. |
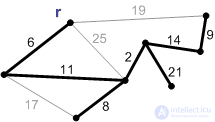 Figure: P8. Ribs weighing 17, 19 and 25 are not safe. Their ends lie in the same connected component. An edge with a weight of 21 is safe, so we add it. The minimum spanning tree has been constructed. |
The running time of Prim's algorithm depends on how the priority queue Ω is implemented. Using a binary heap, initialization on lines 1-4 can be done in O (V) time. Then the cycle is executed | V | times, and each EXTRACT-MIN operation takes O (VlogV) time. The for loop on lines 8-11 takes a total of O (E), since the sum of the degrees of the vertices of the graph is 2 | E |. The membership check in line 9 can be performed in O (1) time if the queue state is also stored as a bit vector of size | V |. The assignment on line 11 implies performing a decrement key operation (DECREASE-KEY), which can take O (logV) time on a binary heap. Thus, in total we get O (VlogV + ElogV) = O (ElogV).
The best estimate can be obtained by using Fibonacci heaps. With Fibonacci heaps, you can perform the EXTRACT-MIN operation in accounting time O (logV), and the DECREASE-KEY operation in accounting time O (1). In this case, the total running time of Prim's algorithm will be O (E + VlogV).
Comments
To leave a comment
Classic algorithms online
Terms: Classic algorithms online