Lecture
Transformations in two-dimensional space are used in various cases: so that individual parts of an object can be described in different coordinate systems; so that typical and repetitive parts can be placed in arbitrary positions in the drawing and in space, including using cycles; so that without re-encoding it was possible to obtain symmetric parts of the object; for the directed deformation of figures, bodies and their parts; for changing the scale of the drawing, building projections of spatial images ... From an analytical point of view, conversion is a recalculation of coordinate values.
A point on the plane is represented by two coordinates: | xy |. The point transformation matrix looks like this:

Below is a point transformation through a square matrix; here x n = xa + yc and y n = xb + yd are the new coordinates of the point after the transformation:
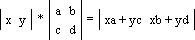
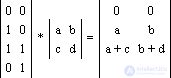
If you imagine a figure as a set of points, then you can also transform it. In the following example, four points are given: A (0, 0), B (1, 0), C (1, 1), D (0, 1), each of which, after conversion, goes to A * (0, 0) , B * (a, b), C * (a + c, b + d), D * (c, d):
Geometrically, this corresponds to the deformation of the figure:
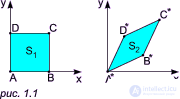
At the same time, the area of the new figure is equal to the area of the old figure multiplied by the determinant of the transformation matrix: S 2 = S 1 * | ad - bc |.
Uniform coordinates. Operations in themAny coordinate system in which the representation of a point in a two-dimensional (three-dimensional) space is specified using three (four) coordinates (P 1 , P 2 , P 3 (, P 4 )) is called a system of homogeneous coordinates. In general, for n-dimensional space, the number of homogeneous coordinates should be one more: n + 1. The use of homogeneous coordinates in the general case allows you to eliminate the anomalies that occur when working in Cartesian coordinates, and to represent complex transformations in the form of a product of several matrices. Geometric interpretation in the case of two-dimensional space: the introduction of a third coordinate equal to one can be interpreted as a transition to a three-dimensional space in which it is allowed to work only in the z = 1 plane. You should imagine that the computer screen (picture plane, image plane) is in the plane z = 1:
In the case of a drawing of the cross section of z = 1, the drawing is forcibly returned to this section so that subsequent operations are possible:
Such an operation is called the normalization of homogeneous coordinates: |
General view of the conversion
Offset operation
The transformation matrix contains the constants m and n , under the action of which the point shifts by m units along the x axis and by n units along the y axis:
Scaling operation
Due to the coefficients a and d of the transformation matrix, there is an increase (or decrease) in the coordinate values of the point (x, y) a and d times along the x and y axes, respectively:
Overall full scaling
In this case, when s <1, the coordinate value of the point (x, y) will increase s times; when s> 1, we get the opposite effect - reducing the value of the coordinates (x, y) by s times. Rotate q
Here q is the angle by which you want to rotate the point (x, y). Please note: rotation occurs relative to the point (0, 0) of the Cartesian coordinate system counterclockwise! And now here is a small task for you. Try to turn the triangle at an angle q = 90 o , the coordinates of the points can take any. Our version is presented here. Display or mirroring
Rotation of a shape around an arbitrary point (m, n) at an arbitrary angle aTo carry out any complex transformation, it is necessary to decompose it into basic operations. Rotating a shape around an arbitrary point (m, n) at an arbitrary angle a consists of three basic operations: 1) transferring the shape to the vector A (-m, -n) to align the point (m, n) with the origin; 2) rotation of the figure at angle a ; 3) transfer of the figure to the vector A '(m, n) to return it to its original position. Since a figure can be represented as a set of points, operations 1) - 3) can be performed sequentially for each point. Let's show it by example. Suppose we want to rotate the triangle with coordinates A (x, y), B (x 1 , y 1 ), C (x 2 , y 2 ) around the point D (m, n) by the angle a . Let P -s be the transfer matrix of a point to the vector A (-m, -n), V a be the rotation matrix for the angle a , P s be the transfer matrix of the point to the vector A '(m, n). So, we have all the data necessary for carrying out a complex transformation of the first point A (x, y): Exactly the same transformations must be carried out for the remaining two points of the triangle, substituting their corresponding coordinates instead of x and y (see the sequence of operations in Figure 1.7). Thus, a complex operation is divided into simplest ones and is given by the product of the corresponding transformation matrices, and the order in which the matrices are multiplied determines the result substantially.
Central projection (perspective)
px + qy + 1 = H - the plane. Notes
Finding the point of intersection of two lines (example)Suppose there are two lines: x + y = 1, 2x - 3y = 0, you need to find the point of their intersection. The solution can be found using matrices. Let's move all members of the equations to the left: x + y - 1 = 0, 2x - 3y - 0 = 0; we write the coefficients of the first equation in the first column of the matrix, the second equation in the second: The condition under which two straight lines intersect looks as follows: To find the answer, both sides of the previous equation must be multiplied to the right of the inverse matrix M -1 (when multiplying M and M -1 , the unit matrix E is obtained):
| xy 1 | = | 3/5 2/5 1 | Answer: the point of intersection of the lines: x = 3/5, y = 2/5. Representation of geometric images in a computerThe Cartesian coordinate system is the basis of numerical modeling of objects. With a few exceptions, all graphic devices work on the basis of this system. If necessary, engineers use other systems (polar, spherical, etc.), and immediately before displaying information on graphic devices, the values can be recalculated. How a point is set, everyone knows, and how are other figures set? A circle is defined by three numbers: the x- and y-coordinates of the center and the radius; for an ellipse, in addition to the coordinates of the center, you need to add the values of its two semi-axes and another direction of one of the axes. The same figure can be set in different ways, but usually they are selected for which the number of parameters is minimal. This minimum number is called the “parametric number of the image.” When compiling programs and algorithms for computer graphics, it is necessary to know the parametric numbers of basic geometric images.
In the task of the object can also participate "logical parameters". You can limit yourself to numbers 0 and 1, or set the parameter by the sign of the number. These parameters do not affect the parametric numbers of objects. For example, a point on a circle can be given by the value of one of its coordinates (X or Y), but it will be necessary to indicate on which semicircle it can be. In computer graphics, it is important from which end the geometric component is drawn, in which case the drawing direction must be specified. This is to determine the visibility of the parties. The direction of the body traversal can be specified by the sign “+” or “-”, you can use tangents, but most often used are tangent vectors, or “direction vectors”. A vector on a plane can be defined by its two projections, the tangent vectors have an arbitrary length — therefore, one can restrict one number, but for convenience, use projections. In fig. 1.1a shows an arc constructed from two end points and the tangent vectors drawn from them. This set (endpoints and tangent vectors) is one of the typical data configurations. If the direction of one of the vectors is reversed, then we will see the picture shown in Fig. 1.1b.
Thus, at the line it will be possible to select two areas ("sides"): "positive", which will be located normal vectors, and "negative". Lines drawn on the surface divide the surface, and surfaces divide the space. This technique is used to solve problems of applying hatching to various elements of a drawing, determining whether a point has a complex shape to the body, or highlight visible or limited parts and surfaces. Ways to represent objectsLet us touch on two different ways of representing geometric objects in a computer. The first method is analytical models. An analytical model is a set of numbers and, if necessary, logical parameters that play the role of coefficients and other quantities in equations, analytical relations that define an object of a given type. For example, for a circle, the main form of the analytical model is the coordinates of the center and the radius, connected by a known relation: (x - x c ) 2 + (y - y c ) 2 - R 2 = 0. A circle, like many other objects, can be defined in a parametric form, where, in addition to coordinates, there is another variable, the parameter. The parametric task of images is widely used in computer graphics. The second method of numerical modeling of geometric objects in computers is coordinate models. In simple cases, these are sets of points that belong to objects and are given by coordinates. For curves and broken lines, points are arranged in the same order as on the line. To arrange points of a surface is a more difficult task: in most cases points are sequentially placed on lines drawn on a surface. Coordinate models have several varieties:
Many graphics devices have linear interpolators. That is, if it is a trajectory-type device, then the image elements are represented as coordinate models, supplemented by control commands. The points sequentially set in them are connected by straight line segments, so all curves are represented as broken lines with small links. This principle allows replacing diverse and analytically complex objects with sets of simple objects. After that, you can perform operations with them using the same algorithms. For some algorithms, consecutive points can be connected by arcs of any curves, which allows to reduce the number of reference points in the model without reducing the accuracy of the representation. |
||||||||||||||||||||||||||||||||||||
Comments
To leave a comment
computer graphics
Terms: computer graphics