Lecture
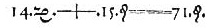
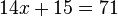 )
) Equation is equality of type
Most often in quality  numerical functions appear, although in practice there are more complex cases - for example, equations for vector functions, functional equations, etc.
numerical functions appear, although in practice there are more complex cases - for example, equations for vector functions, functional equations, etc.
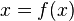
The solution of the equation is the task of finding such argument values for which this equality is achieved. Additional conditions (integer, realness, etc.) may be imposed on the possible values of the arguments.
Arguments of given functions (sometimes called “variables”) in the case of an equation are called “unknowns”.
The values of the unknowns at which this equality is achieved are called solutions or the roots of a given equation.
Pro roots say they satisfy this equation.
To solve an equation means to find the set of all its solutions (roots) or to prove that there are no roots.
Equivalent or equivalent are called equations whose root sets coincide. Equivalents are also considered to be equations that have no roots.
Equivalence of equations has the symmetry property: if one equation is equivalent to another, then the second equation is equivalent to the first.
Equivalence of equations has the property of transitivity: if one equation is equivalent to another, and the second is equivalent to the third, then the first equation is equivalent to the third. The equivalence property of equations allows to carry out transformations with them, on which the methods of their solution are based.
The third important property is given by the theorem: if the functions  are given over the integrity domain, then the equation
are given over the integrity domain, then the equation
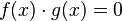
is equivalent to a set of equations:

This means that all the roots of the first equation are the roots of one of the other two equations and allows you to find the roots in parts.
With algebraic expressions included in the equations, you can perform operations that do not change its roots, in particular:
The equations that result from these operations are equivalent to the initial equation. However, for properties 4 and 5, there is a restriction: if the same expression is added to both sides of the equation (or if the same expression is subtracted from both sides of the equation), which contains the unknown and loses its meaning, the unknown takes the values of the roots of this equation , the equation turns out to be nonequivalent to the original (initial) one. But if we add the same expression to both sides of the equation (or subtract the same expression from both sides of the equation), which contains the unknown and loses meaning only for the values of the unknown, which are not the roots of this equation, we get an equation equivalent to the initial one.
Multiplying or dividing both sides of an equation by an expression containing an unknown can, respectively, lead to the appearance of extraneous roots or loss of roots.
Squaring both sides of the equation can result in extraneous roots.
The equation
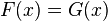
called the consequence of the equation
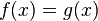 ,
, if all the roots of the second equation are the roots of the first. The first equation may have additional roots, which are called extraneous for the second equation. Extraneous roots may appear during the transformations necessary to find the roots of equations. In order to detect them, it is necessary to check the root by substituting into the original equation. If, during the substitution, the equation becomes an identity, then the root is real, if not - an outsider.
The equation
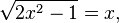
during the construction of both parts in the square gives the equation
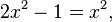 or
or 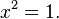
Both equations are a consequence of the original. The last one is easy to solve. It has two roots
 and
and 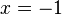 .
. When substituting the first root in the original equation forms the identity
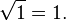
When substituting another root, an incorrect statement is obtained:
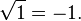 .
. Thus, the second root must be discarded as an outsider.
There are algebraic, parametric, transcendental, functional, differential and other types of equations.
Some classes of equations have analytical solutions that are convenient in that they not only give the exact value of the root, but allow you to write the solution in the form of a formula, which may include parameters. Analytical expressions allow not only to calculate the roots, but to analyze their existence and their number depending on the values of the parameters, which is often even more important for practical application than the specific values of the roots.
The equations for which analytical solutions are known include algebraic equations, not exceeding the fourth degree: a linear equation, a quadratic equation, a cubic equation, and a fourth degree equation. Algebraic equations of higher degrees in the general case have no analytical solution, although some of them can be reduced to equations of lower degrees.
Equations that include transcendental functions are called transcendental. Among them, analytical solutions are known for some trigonometric equations, since the zeros of trigonometric functions are well known.
In the general case, when an analytical solution cannot be found, numerical methods are used. Numerical methods do not provide an exact solution, but only allow narrowing the interval in which the root lies to a certain predetermined value.
Algebraic equation is called the equation
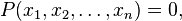
Where 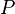 - polynomial of variables
- polynomial of variables 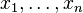 that are called unknowns.
that are called unknowns.
Polynomial coefficients 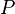 usually taken from some field
usually taken from some field 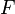 and then the equation
and then the equation 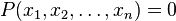 called an algebraic equation over a field
called an algebraic equation over a field 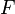 . The degree of an algebraic equation is the degree of a polynomial.
. The degree of an algebraic equation is the degree of a polynomial. 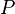 .
.
For example, the equation
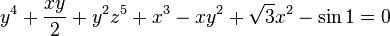
is a seventh degree algebraic equation of three variables (with three unknowns) over the field of real numbers.
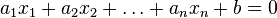
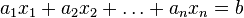

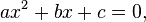
Where 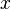 - free variable
- free variable 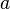 ,
,  ,
,  - coefficients, and
- coefficients, and 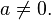
Expression 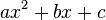 called the square three-member . The root of such an equation (quadratic root) is the value of the variable
called the square three-member . The root of such an equation (quadratic root) is the value of the variable 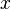 which squares the quadruple to zero, that is, the value that squares the equation into an identity. The coefficients of the quadratic equation have their own names: coefficient
which squares the quadruple to zero, that is, the value that squares the equation into an identity. The coefficients of the quadratic equation have their own names: coefficient 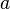 called the first or highest coefficient
called the first or highest coefficient  called the second or coefficient of
called the second or coefficient of 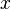 ,
,  called the free member of this equation. Given quadratic equation is called, in which the leading coefficient is equal to one. Such an equation can be obtained by dividing the whole expression by the highest coefficient
called the free member of this equation. Given quadratic equation is called, in which the leading coefficient is equal to one. Such an equation can be obtained by dividing the whole expression by the highest coefficient 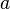 :
: 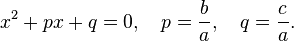 A complete quadratic equation is called such, all coefficients of which are non-zero. An incomplete quadratic equation is one in which at least one of the coefficients except the highest one (either the second coefficient or the free term) is zero. The graph of the quadratic function is a parabola.
A complete quadratic equation is called such, all coefficients of which are non-zero. An incomplete quadratic equation is one in which at least one of the coefficients except the highest one (either the second coefficient or the free term) is zero. The graph of the quadratic function is a parabola.
To find the roots of a quadratic equation 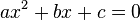 In general, the following algorithm should be used:
In general, the following algorithm should be used:
1) if 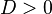 | 2) if 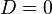 | 3) if 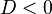 |
there are two roots, for finding use the formula: 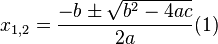 , , | the root is one (in some contexts they also speak of two equal or coincident roots — it is also called a root of multiplicity 2 ), whose formula is 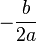 | conclude that there are no roots on the set of real numbers. |
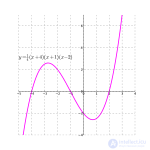
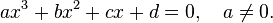
For a graphical analysis of the cubic equation in the Cartesian coordinate system, a cubic parabola is used.
Any cubic equation of the canonical form can be reduced to a simpler form:
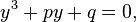
dividing it by 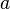 and substituting a replacement for it
and substituting a replacement for it 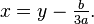 In this case, the coefficients will be equal to:
In this case, the coefficients will be equal to:
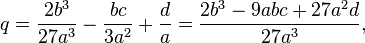
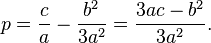
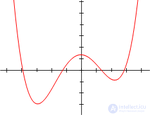
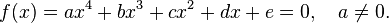
The fourth degree for algebraic equations is the highest, for which there is an analytical solution in radicals in a general form (that is, for any value of coefficients).
Because  is a polynomial of even degree, it has the same limit as it tends to plus and minus infinity. If a
is a polynomial of even degree, it has the same limit as it tends to plus and minus infinity. If a 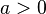 , the function increases to plus infinity on both sides, so the function has a global minimum. Similarly, if
, the function increases to plus infinity on both sides, so the function has a global minimum. Similarly, if  , the function decreases to minus infinity on both sides, thus the function has a global maximum.
, the function decreases to minus infinity on both sides, thus the function has a global maximum.
The system of equations of the form:
| (one) |
Here 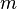 - the number of equations, and
- the number of equations, and 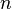 - number of unknowns. x 1 , x 2 , ..., x n - unknowns that need to be determined. a 11 , a 12 , ..., a mn - the coefficients of the system - and b 1 , b 2 , ... b m - free members - are assumed to be known. The indices of the coefficients ( a ij ) of the system denote the numbers of the equation ( i ) and the unknown ( j ) at which this coefficient stands, respectively [1] .
- number of unknowns. x 1 , x 2 , ..., x n - unknowns that need to be determined. a 11 , a 12 , ..., a mn - the coefficients of the system - and b 1 , b 2 , ... b m - free members - are assumed to be known. The indices of the coefficients ( a ij ) of the system denote the numbers of the equation ( i ) and the unknown ( j ) at which this coefficient stands, respectively [1] .
A system is called homogeneous if all its free terms are equal to zero ( b 1 = b 2 = ... = b m = 0), otherwise - non-homogeneous. A system is called square if the number m of equations equals the number n of unknowns. The solution of the system is the set of n numbers c 1 , c 2 , ..., c n such that the substitution of each c i instead of x i into the system turns all its equations into identities. A system is called joint if it has at least one solution, and incompatible if it does not have a single solution. Solutions c 1 (1) , c 2 (1) , ..., c n (1) and c 1 (2) , c 2 (2) , ..., c n (2) of the joint system are called different if at least one is violated from equalities:
| c 1 (1) = c 1 (2) , c 2 (1) = c 2 (2) , ..., c n (1) = c n (2) . |
A collaborative system is called defined if it has a single solution; if she has at least two different solutions, then it is called indefinite. If there are more equations than unknowns, it is called overdetermined.
An equation with parameters is a mathematical equation, the appearance and solution of which depends on the values of one or several parameters. Solving an equation with a parameter means:
Equations with a parameter can be both linear and nonlinear.
An example of a linear equation with a parameter:
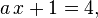
An example of a nonlinear equation with a parameter:
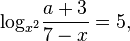
Where 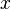 - independent variable
- independent variable 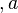 - parameter.
- parameter.
A transcendental equation is an equation that is not algebraic. These are usually equations containing exponential, logarithmic, trigonometric, inverse trigonometric functions, for example:
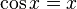
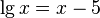
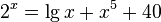
A more rigorous definition is: a transcendental equation is an equation of the form 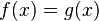 where functions
where functions 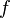 and
and 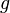 are analytic functions, and at least one of them is not algebraic.
are analytic functions, and at least one of them is not algebraic.
A functional equation is an equation expressing the relationship between the value of a function (or functions) at one point and its values at other points. Many properties of functions can be determined by examining the functional equations that these functions satisfy. The term functional equation is usually used for equations that cannot be reduced to simple algebraic equations. This irreducibility is most often due to the fact that the arguments of the unknown function in the equation are not the independent variables themselves, but some of these functions from them. For example:
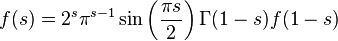
 - Euler's gamma function satisfies the Riemann Zeta function.
- Euler's gamma function satisfies the Riemann Zeta function. 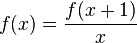

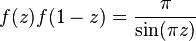 (Euler addition formula)
(Euler addition formula) 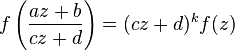
 , defines f as a modular form of order k .
, defines f as a modular form of order k . A differential equation is an equation connecting the value of a certain unknown function at a certain point and the value of its derivatives of different orders at the same point. The differential equation contains in its record an unknown function, its derivatives, and independent variables. The order of a differential equation is the largest order of derivatives entering into it. The solution of a differential equation of order n is the function y (x) , which has derivatives on some interval (a, b) 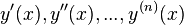 up to order n inclusive and satisfying this equation. The process of solving a differential equation is called integration.
up to order n inclusive and satisfying this equation. The process of solving a differential equation is called integration.
All differential equations can be divided into
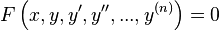 or
or 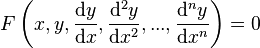 ,
, Where 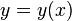 — неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от независимой переменной
— неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от независимой переменной  , штрих означает дифференцирование по
, штрих означает дифференцирование по  .
.
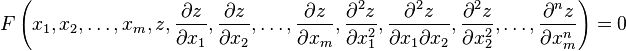 ,
, Where 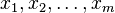 — независимые переменные, а
— независимые переменные, а 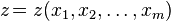 — функция этих переменных.
— функция этих переменных.
Первоначально дифференциальные уравнения возникли из задач механики, в которых участвовали координаты тел, их скорости и ускорения, рассматриваемые как функции времени.
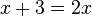
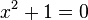
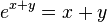
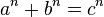 where
where 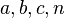 — натуральные числа
— натуральные числа
Comments
To leave a comment
introduction to math. the basics
Terms: introduction to math. the basics