Lecture
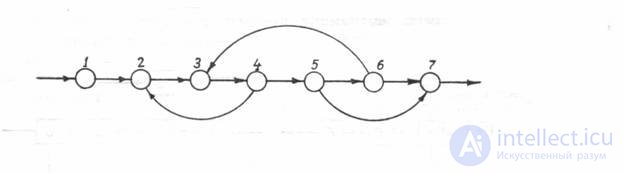
Fig. 1. Oriented graph
A sequence of concatenated arcs that allows one to go from one vertex to another is called a path. So, on the graph under consideration, from the vertex 1 to the vertex 4 there will be a sequence of arcs 1-2, 2-3, 3-4. A path can also be represented by a sequence of vertices that contains them, for example, the path 1,2,3,4,3 or the path 1, 2, 3, 4, 5. The length of the path is the number of arcs on the path. For example, the path from vertex 1 to vertex 7 has a length of 6.
The path whose initial vertex coincides with the final vertex, and each vertex, with the exception of the initial one, is traversed once, is called a contour. In the graph under consideration, the following contours can be distinguished:
(2, 3.4, 2), (3,4,3), (6, 7.6). ????
The contours of the graph, having at least one common vertex, are called connected . The system of connected graph contours forms a complex. For any two vertices belonging to the complex, there is a connecting path. So, contours (2, 3, 4, 2) and (3. 4, 3) are 'connected, since they have at least one common vertex, for example, vertex 3 (or vertex 4), therefore vertices 2 , 3, 4 form a complex. It is easy to verify that for any two vertices of this complex there is a connecting path. For example, take two vertices 2 and 4. From vertex 2 to vertex 4 leads the path 2.-3.3-4, and from vertex 4 to the vertex 2 - path 4-2. The complex corresponds to elements that can only be calculated jointly.
Algorithms for extracting complexes use the main property of the vertices of the graph belonging to the complex for any two vertices I and J included in the complex, there must be a path from the I to the Jth vertex and the return path from the J to the Ith vertex (naturally in the direction of oriented arcs). To isolate complexes, there are various matrix algorithms [1-3]. Some of them are related to the representation of the structure of the CTS as a communication matrix and the subsequent operations with this matrix in order to select paths of various lengths on the CTS graph and to construct the complex matrix.
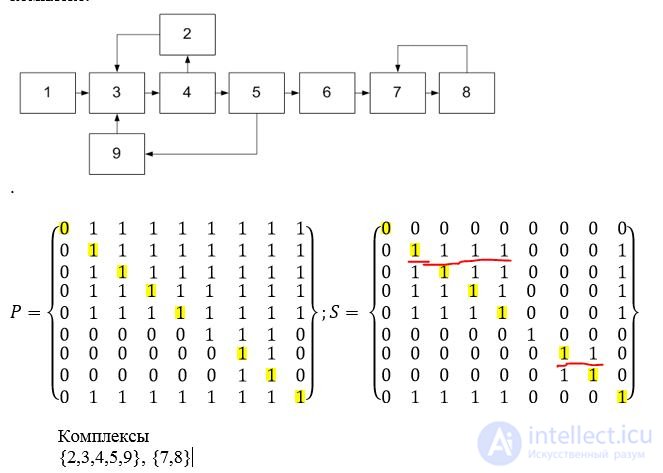
The basis of other algorithms is the use of a matrix of paths on a graph. The matrix of paths is square and contains as many columns as there are elements in the composition of the HTS. If on the graph there is a path of any length from vertex I to vertex J, then 1 is placed at the intersection of the I-th row and the J-th column of the path matrix, otherwise it is 0. On the main diagonal of this matrix, one is put, since the path is considered to be 0 from any element in the same element always exists. The mattress of the paths of the XTS graph shown in fig. 2 (we denote this matrix by the letter P), has the form:
|
P =
|
one |
one |
one |
one |
one |
one |
one |
|
0 |
one |
one |
one |
one |
one |
one |
|
|
0 |
one |
one |
one |
one |
one |
one |
|
|
0 |
one |
one |
one |
one |
one |
one |
|
|
0 |
0 |
0 |
0 |
one |
one |
one |
|
|
0 |
0 |
0 |
0 |
0 |
one |
one |
|
|
0 |
0 |
0 |
0 |
0 |
one |
one |
Along with the matrix P, an auxiliary matrix S is constructed. It is transposed with respect to the matrix P, that is, the columns of the matrix S are the rows of the matrix P:
|
S =
|
one |
0 |
0 |
0 |
0 |
0 |
0 |
|
one |
one |
one |
one |
0 |
0 |
0 |
|
|
one |
one |
one |
one |
0 |
0 |
0 |
|
|
one |
one |
one |
one |
0 |
0 |
0 |
|
|
one |
one |
one |
one |
one |
0 |
0 |
|
|
one |
one |
one |
one |
one |
one |
one |
|
|
one |
one |
one |
one |
one |
one |
one |
The elements of the matrix P indicate the presence of a path from the I vertex to the Jth vertex, and the elements of the matrix S from the Jth vertex to the 1st. Logically multiplying the elements of the matrices P and S (assuming 0 * 0 = 0, 0 * 1 = 0, 1 * 0 = 0, 1 * 1 = 1), we obtain the matrix D of the allocation of complexes:
|
D =
|
one |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
one |
one |
one |
0 |
0 |
0 |
|
|
0 |
one |
one |
one |
0 |
0 |
0 |
|
|
0 |
one |
one |
one |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
one |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
one |
one |
|
|
0 |
0 |
0 |
0 |
0 |
one |
one |
Using the matrix D, we determine the complexes that are part of the XTS graph, according to the following rules:
- if in the I-th row of this matrix there is only one non-zero element d (1,1) = 1 (belonging to the main diagonal), then the XTS element with the number I can be calculated separately from the other elements of the system. In this example, these are elements 1 and 5.
- rows of the matrix D, having, in addition to the element d (1,1), other non-zero elements, correspond to complexes. Non-zero line items indicate the vertices of the graph that make up the complex.
In our example, according to matrix D, two complexes are part of the CTS:
complex 1 - (2, 3, 4) and complex 2 - (6, 7).
The same rows of the matrix correspond to the same complex.
Example 2
Consider any three vertices of the XTC graph: I, J, M. If there is a path of any length from vertex I to vertex J and from vertex J to I, then these vertices belong to the same complex K. To attach the vertex M to the complex, you must analyze , is there a path from any vertex (for example, I belonging to the complex K, to the vertex M and a return path from the vertex M to any vertex of the complex K (for example, I). If these two paths exist, then the vertex M belongs to the complex K
The application of this rule to the HTS depicted in Fig. 3, allows to distinguish the following complexes: - complex K1- (1,2, 3, 8, 9, 10), complex K2 - (5.11), elements 4,6, 7 are calculated autonomously.
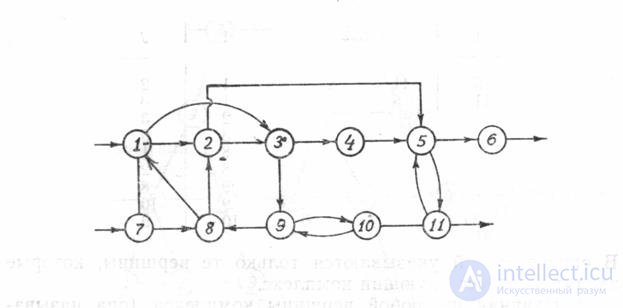
Fig. 2. Count some closed HTS
Determination of the preliminary sequence of calculation of the HTS.
After isolating the complexes, a preliminary sequence for calculating the CTS is determined. The set of vertices included in the complex is combined into one new vertex, as a result of which a graph is obtained that does not contain contours (Fig. 3).
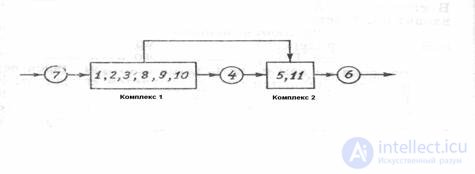
Fig.3. The definition of PPRS.
Such a graph corresponds to open XTS. Therefore, the determination of the preliminary sequence of the calculation of the closed system (PPRS) is performed according to the algorithms used in the structural analysis of open XTS.
For the considered system we have: PPRS - [7, (1, 2. 3, 8, 9, 10), 4, (5, 11), 6]
example 3
The structure of CTS is usually considered in terms of graph theory, i.e. in the form of a directed graph, the vertices of which correspond to the apparatus, and the arcs to the flows (for example, as in Fig. 4.2). In Figure 4.2.2, the numbers of the vertices are indicated by a large italic (to the right above the top of the vertex), and the numbers of the streams are indicated by a small regular font (under the line of the corresponding stream).
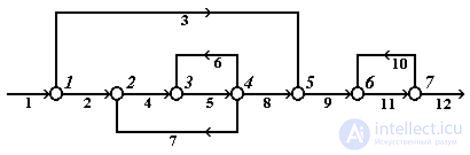
Fig.4.2. Representation of the CTS in the form of a directed graph
A sequence of concatenated arcs that allows one to go from one vertex to another is called a path. The path can be designated both through a sequence of arcs, and through a sequence of vertices. The path whose initial vertex coincides with the final vertex, and each vertex, with the exception of the initial vertex, is traversed only once, is called a contour. For example, in Fig. 4.2 there are three contours (at the vertices): 2-3-4-2, 3-4-3 and 6-7-6.
A complex is a part of a graph whose vertices have the following properties:
- each of the vertices and arcs of the complex is included in one of the contours of the graph;
- if the vertex i enters the complex, then this complex also includes all the vertices included in the contours that contain the vertex i.
For example, on the graph presented in Fig. 4.2 there are two complexes (at the vertices): 2-3-4 and 6-7. The first complex consists of two circuits (2-3-4-2 and 3-4-3), and in the second - one (6-7-6).
example 4
Comments
To leave a comment
System analysis (systems philosophy, systems theory)
Terms: System analysis (systems philosophy, systems theory)