The system of m linear equations:
a
m 1 x
1 + a
m 2 x
2 + ... + a
m n x
n = b
m , m = 1, 2, ..., n.
A system of n linear equations with n unknowns can be rewritten as:
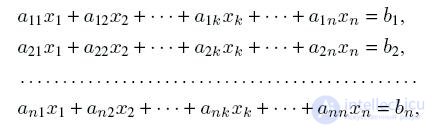
where a
11 , a
12 , ..., and
nn are coefficients, b
1 , b
2 , ..., b
n are free members and x
1 , x
2 , ..., x
n are unknown.
The set of n numbers x
1 , ..., x
n , which, being substituted into the original system, turn equations into identities, is called a solution of the system. A system that has at least one solution is called a joint. A system that does not have a solution at all is called incompatible.
Cramer's Rule If the determinant of the system is nonzero

the system has the only solution sought by Cramer’s rule:
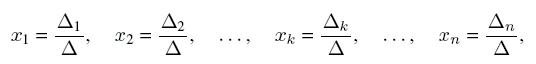
where det
k is the determinant obtained by replacing the
kth column of the original determinant of the system by the column of free terms:

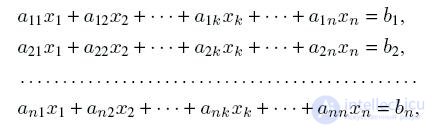

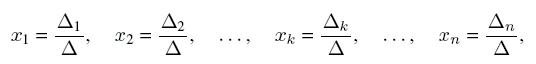

Comments
To leave a comment
HANDBOOK ON MATHEMATICS, SCHOOL MATHEMATICS, HIGHER MATHEMATICS
Terms: HANDBOOK ON MATHEMATICS, SCHOOL MATHEMATICS, HIGHER MATHEMATICS